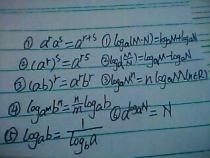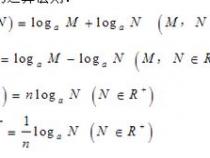log对数函数基本十个公式是什么呢

一、log对数函数基本十个公式是什么呢

1、log(a)(MN)=log(a)(M)+log(a)(N)；

2、log(a)(M/N)=log(a)(M)-log(a)(N)；

3、log(a)(M^n)=nlog(a)(M)（n∈R）；

4、log(A)M=log(b)M/log(b)A(b>0且b≠1）；

5、对数恒等式：a^log（a)N=N，log（a）a^b=b；

6、log(a)M^(1/n)=(1/n)log(a)M；

7、log(a)M^(-1/n)=(-1/n)log(a)M；

10、log(a)b×log(b)c×log(c)a=1。

1、若式中幂指数则有以下的正数的算术根的对数运算法则，一个正数的算术根的对数，等于被开方数的对数除以根指数。

2、定义域x为真数，真数必须为正数，故定义域为{x|x>0}。每次进行拆分时保证每个真数为正数，如log2(-2*(-4)）不能拆分，但是其本身可以计算。

3、以10为底的对数函数通常记为lg，以自然数e（大约为2.718）为底的对数函数，通常记为ln。

二、log对数函数基本十个公式是什么

7、Iog(A*B*C)=logA+logB+logC。logA'n=nlogA。

9、log(a)(MN)=log(a)(M)+log(a)(N)。

10、Iog(A)M=log(b)M/log(b)A(b>0Eb#1)。

在数学中，对数是对求幂的逆运算，正如除法是乘法的倒数，反之亦然。这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。在简单的情况下，乘数中的对数计数因子。

更一般来说，乘幂允许将任何正实数提高到任何实际功率，总是产生正的结果，因此可以对于b不等于1的任何两个正实数b和x计算对数。

三、log函数基本十个公式

log函数基本十个公式包括：log_a(mn)=log_a m+log_a n，log_a(m/n)=log_a m-log_a n，log_a(m^n)=n*log_a m，log_a(1/m)=-log_a m等。

log函数基本十个公式包括：log_a(mn)=log_a m+log_a n，log_a(m/n)=log_a m-log_a n，log_a(m^n)=n* log_a m，log_a(1/m)=-log_a m，log_a(a^m)=m，log_a(sqrt(m))=log_a m/2，log_b(b^n)=n，log_e(e^n)=n，log_10(10^n) n，以及换底公式log_b a=log_c a/log_c b。

包括对数乘法法则、除法法则、指数法则和对数换底公式。这些法则在计算对数时非常有用，可以简化复杂的对数计算。

换底公式是log_b a=log_c a/log_c b，其中b和c是任意正实数且c≠1。换底公式允许改变对数的底数，以便进行更简单的计算。

包括对数的定义域和值域、对数的真数性质和对数的底数性质。

对数不等式是数学中一个重要的概念，涉及到对数函数和不等式的性质。通过掌握对数不等式的解法，可以解决一些实际问题，如在金融、统计学和物理学等领域中的应用。

对数方程是数学中另一个重要的概念，涉及到对数函数和方程的性质。对数方程的解法可以解决一些实际问题，如在化学、生物学和工程学等领域中的应用。