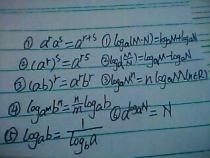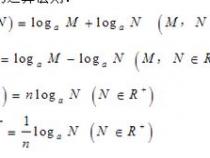高中数学对数公式大全

一、高中数学对数公式大全

1、对数运算法则：a^log（a）N=N（a>0且a不等于1)）log（a）^n=n（a>0且a不等于1）log（a）MN=log（a）M+log（a）N（a>0月a不等于1）。log（a）M/N=log（a）M-log（a）N（a>0月a不等于1）。log（a）^M^n=nlog（a）^M（a>0月a不等于1）。

2、对数函数的运算性质：如果a=em，那么m称为以a为底e的对数，记作logea=m，e为自然对数的底数，其为无限不循环小数，定义如下：若an=b(a>0，a不等于1)，则n=logea。

在数学中，对数是对求幂的逆运算，正如除法是乘法的逆运算，反之亦然。这意味着一个数字的对数是必须产生另一个固定数字（基数）的指数。在简单的情况下，乘数中的对数计数因子。

更一般来说，乘幂允许将任何正实数提高到任何实际功率，总是产生正的结果，因此可以对于b不等于1的任何两个正实数b和x计算对数。

对数在数学内外有许多应用。这些事件中的一些与尺度不变性的概念有关。例如，鹦鹉螺的壳的每个室是下一个的大致副本，由常数因子缩放。这引起了对数螺旋。Benford关于领先数字分配的定律也可以通过尺度不变性来解释。对数也与自相似性相关。

例如，对数算法出现在算法分析中，通过将算法分解为两个类似的较小问题并修补其解决方案来解决问题。自相似几何形状的尺寸，即其部分类似于整体图像的形状也基于对数。对数刻度对于量化与其绝对差异相反的值的相对变化是有用的。

此外，由于对数函数log(x)对于大的x而言增长非常缓慢，所以使用对数标度来压缩大规模科学数据。对数也出现在许多科学公式中，例如Tsiolkovsky火箭方程，Fenske方程或能斯特方程。

二、对数函数有哪些公式

1、对数函数是数学中的一类重要函数，它有许多基本性质和常用公式。以下是一些对数函数的常见公式：

2、定义式：log(a)(b)= ln(b)/ ln(a)（a> 0，且a≠ 1）。

3、互换律：log(a)(b)= log(b)(a)。

4、加法性质：log(a)(b+ c)= log(a)(b)+ log(a)(c)。

5、乘法性质：log(a)(b* c)= log(a)(b)+ log(a)(c)。

6、指数和对数的关系：aloga(b)= b（a> 0，且a≠ 1）。

7、换底公式：log(a)(b)= ln(b)/ ln(a)= log(c)(b)/ log(c)(a)（c> 0，且c≠ 1）。

8、对数的运算性质：log(a)(b)* log(b)(a)= 1（a> 0，且a≠ 1）。

9、对数的恒等式：log(a)(M* N)= log(a)(M)+ log(a)(N)。

10、对数的运算律：log(a)(M* N)= log(a)(M)+ log(a)(N)，log(a)(M/ N)= log(a)(M)- log(a)(N)。

11、以上是对数函数的一些常用公式，掌握这些公式可以帮助你更好地理解和运用对数函数。

三、对数函数公式有哪些

1、log(a)(MN)=log(a)(M)+log(a)(N);

2、log(a)(M/N)=log(a)(M)-log(a)(N);

3、log(a)(M^n)=nlog(a)(M)（n∈R）

4、log(a^n)(M)=1/nlog(a)(M)(n∈R)

5、换底公式：log(A)M=log(b)M/log(b)A(b>0且b≠1）

7、对数恒等式：a^log（a)N=N; log（a）a^b=b

同底的对数函数与指数函数互为反函数。

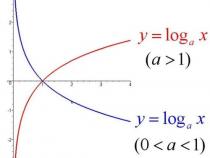
对数函数的一般形式为 y=㏒ax，它实际上就是指数函数的反函数（图象关于直线y=x对称的两函数互为反函数），可表示为x=ay。因此指数函数里对于a的规定（a>0且a≠1），右图给出对于不同大小a所表示的函数图形：

关于X轴对称、当a>1时，a越大，图像越靠近x轴、当0<a<1时，a越小，图像越靠近x轴。

可以看到，对数函数的图形只不过是指数函数的图形的关于直线y=x的对称图形，因为它们互为反函数。

参考资料来源：百度百科-对数函数