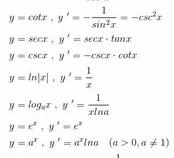什么是对数函数和指数函数

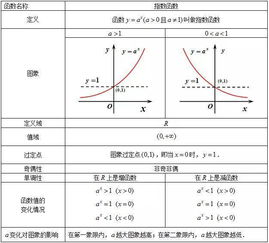
一、什么是对数函数和指数函数

对数函数和指数函数中各部分的名称如下：

在对数函数中，通常有以下要素：

1.底数（base）：对数函数中的底数指的是对数的基准，决定了对数函数的性质和变化规律。

2.真数（antilogarithm）：对数函数中的真数是指对数运算的结果，即所要求取对数的数值。

3.对数（logarithm）：对数函数中的对数指的是将底数变为真数所需的指数。对数函数的一般表达式为 y= logₐ(x)，表示以底数 a对 x进行对数运算。

在指数函数中，通常有以下要素：

1.底数（base）：指数函数中的底数指的是指数运算的基准。

2.指数（exponent）：指数函数中的指数是对底数进行幂运算的数值，决定了指数函数的增长速度和变化规律。

3.幂（power）：指数函数中的幂指的是底数进行指数运算的结果。指数函数的一般表达式为 y= a^x，表示底数 a的指数运算结果为 y。

需要注意的是，在不同的数学符号和符号约定中，对数和指数函数的表示方式可能会有所不同。常用的对数函数有以 10为底的常用对数（logarithm，通常用 log表示）和以 e为底的自然对数（natural logarithm，通常用 ln表示）。而常用的指数函数有以 10为底的指数函数（exponential function，通常用 exp表示）和以 e为底的自然指数函数（natural exponential function，通常用 e^x表示）。

对数和指数函数在数学和科学领域中有广泛的应用，能够描述和解决各种与变化率、增长速度、比例关系等相关的问题。

二、幂函数和对数函数之间有什么关系

对数函数和幂函数是数学中常见的两种函数，它们之间存在转换关系。这里介绍一下对数函数和幂函数之间的转换：

1.幂函数转对数函数：对于幂函数 y= a^x（其中 a是正实数且不等于 1），可以通过对函数取对数得到对数函数。具体而言，可以将幂函数转化为以底为 a的对数函数。例如，对于函数 y= 2^x，将其取以 2为底的对数，则有 log2(y)= x。

2.对数函数转幂函数：对于以 a为底的对数函数 y= loga(x)（其中 a是正实数且不等于 1），可以通过对函数取幂，将其转化为幂函数。具体而言，可以将对数函数转化为底为 a的幂函数。例如，对于函数 y= log2(x)，可以将其转化为 y= 2^x。

这种转换关系可以在解决一些数学问题和方程中发挥作用。通过将幂函数转换为对数函数，可以简化问题的求解过程；而通过将对数函数转换为幂函数，可以将问题转化为常规的幂函数求解。

对数函数和幂函数的转换关系在数学和应用中都有广泛的应用。它们互为逆运算，允许我们在两种函数之间进行灵活的转换和运用

三、对数函数和幂函数之间的关系是什么

1、对数函数和幂函数之间的转换公式为：log(a)(MN)=Nlog(a)(M)，其中a为底数，M为幂函数，N为指数。

2、这个公式可以用来将幂函数的形式转换为对数函数的形式，也可以将和对数函数的形式转换为幂函数的形式。具体来说，如果已知一个幂函数M和它的指数N，以及一个底数a，可以使用上述公式将幂函数转换为对数函数。例如，如果M=x2，N=3，a=10，则可以使用公式log(a)(MN)=Nlog(a)(M)计算出：

3、如果已知一个对数函数log(a)(M)，以及一个底数a和真数M，可以使用上述公式将和对数函数转换为幂函数。例如，如果log(a)(M)=2，a=10，M=100，则可以使用公式log(a)(MN)=Nlog(a)(M)计算出：

4、因此，对数函数和幂函数之间的转换公式可以帮助我们在两种函数形式之间进行转换。