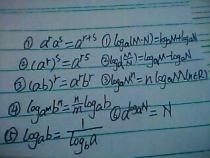解二次函数公式

发布时间:2025-05-24 17:01:43 发布人:远客网络

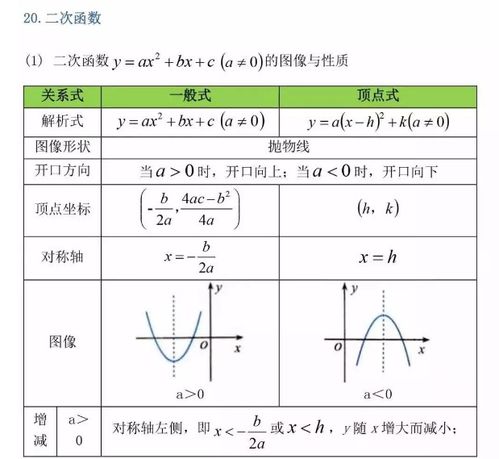
解二次函数公式

一、解二次函数公式

1、求根公式（任何一个均二次函数都可以）:Δ=b^2-4ac,根的判别式（若Δ<0,此方程无实数解；若Δ=0，此方程有且只有一个解；若Δ>0，此方程有2个不同的解）

2、十字相乘法：f(x)=(kx+a)(kx+b）

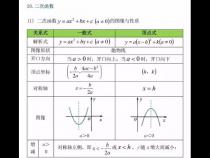
3、二次函数（quadratic function）的基本表示形式为y=ax²+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

4、二次函数表达式为y=ax²+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。

5、如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。

6、一般地，把形如（a、b、c是常数）的函数叫做二次函数，其中a称为二次项系数，b为一次项系数，c为常数项。x为自变量，y为因变量。等号右边自变量的最高次数是2。

7、顶点坐标交点式为（仅限于与x轴有交点的抛物线），与x轴的交点坐标是和。

8、注意：“变量”不同于“未知数”，不能说“二次函数是指未知数的最高次数为二次的多项式函数”。“未知数”只是一个数（具体值未知，但是只取一个值），“变量”可在一定范围内任意取值。

9、在方程中适用“未知数”的概念（函数方程、微分方程中是未知函数，但不论是未知数还是未知函数，一般都表示一个数或函数——也会遇到特殊情况），但是函数中的字母表示的是变量，意义已经有所不同。从函数的定义也可看出二者的差别。

二、函数公式有哪些

1、函数公式有很多种，以下是几种常见的函数公式：

2、线性函数是最基础的函数类型之一，其中y是输出值，m是斜率，b是截距。线性函数公式描述了输入值x与输出值y之间的线性关系。

3、二、二次函数公式：y= ax²+ bx+ c

4、二次函数是一种描述二次关系的函数。其中a、b和c为常数，a不等于0。这个公式描述了变量x的二次方程关系与输出值y之间的关系。

5、三、三角函数公式：如正弦函数（sin x）、余弦函数（cos x）、正切函数（tan x）等。

6、三角函数在三角学和数学分析中有着广泛的应用。这些函数描述了角度与边长之间的关系，常用于解决与圆有关的问题。

7、四、对数函数公式：y= log(x)或 y= ln(x)（自然对数）等。

8、对数函数描述的是幂运算的逆运算。在数据处理和计算中，对数函数常用于简化计算过程。

9、五、指数函数公式：y= a^x（其中a大于0且a不等于1）。

10、指数函数描述的是数的乘方运算。在计算机科学、金融等领域，指数函数有着广泛的应用。

11、六、幂函数公式：y= x^n（n为实数）。幂函数描述的是变量x的n次方与输出值y之间的关系。幂函数的图像会根据n的值呈现出不同的形状。这些只是部分常见的函数公式，实际上还有更多复杂的函数公式，如多项式函数、分段函数等。不同的函数公式在数学、物理和工程等领域都有广泛的应用。学习和掌握这些函数公式对于理解和解决实际问题具有重要意义。