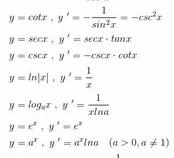指数函数的应用场景有哪些

一、指数函数的应用场景有哪些

指数函数是数学中一种常见的函数形式，其应用场景非常广泛。以下是一些常见的指数函数应用场景：

1.金融领域：在金融领域中，指数函数被广泛应用于计算复利、利率、股票价格等。例如，复利的计算公式就是一个指数函数的形式。

2.生物学和医学：在生物学和医学中，指数函数被用于描述生物种群的增长、细胞分裂、药物代谢等过程。这些过程通常呈现出指数增长或衰减的趋势。

3.物理学：在物理学中，指数函数被用于描述放射性衰变、光的传播、声音的传播等现象。例如，放射性衰变的速率通常可以用指数函数来描述。

4.工程学：在工程学中，指数函数被用于描述信号传输、电路分析、材料老化等过程。例如，电路中的电容充电和放电过程可以用指数函数来描述。

5.统计学：在统计学中，指数函数被用于描述数据的分布和概率密度函数。例如，正态分布的概率密度函数就是一个指数函数的形式。

6.经济学：在经济学中，指数函数被用于描述经济增长、通货膨胀、失业率等经济指标的变化趋势。这些指标通常呈现出指数增长或衰减的特点。

二、指数函数可以用于解决哪些数学问题

指数函数是数学中非常重要的一类函数，可以用于解决许多实际问题和数学问题。以下是一些常见的应用：

1.增长模型：指数函数可以用来描述人口、经济增长、病毒传播等具有指数增长趋势的现象。通过建立适当的指数增长模型，可以预测未来的发展趋势。

2.衰减模型：指数函数也可以用来描述物质的衰减过程，如放射性衰变、声音的传播等。衰减模型可以帮助我们理解物质随时间的减少规律。

3.复利计算：在金融领域，指数函数被广泛应用于复利计算。复利是指利息不仅基于本金，还基于之前产生的利息。通过使用指数函数，可以计算出复利的增长速度和最终金额。

4.生物学和医学：指数函数在生物学和医学中也有广泛应用。例如，在种群生态学中，指数函数可以描述物种的增长和扩散；在药物治疗中，药物的浓度通常按照指数方式减少。

5.化学反应速率：化学反应速率通常与反应物浓度的指数函数成正比。通过建立适当的指数函数模型，可以研究化学反应的动力学特性。

6.信号处理：在信号处理中，指数函数常用于描述信号的衰减和滤波过程。例如，音频信号的衰减通常可以用指数函数来建模。

7.统计学：指数分布是一种常见的概率分布，广泛应用于统计学中。它可以用来描述等待时间、寿命等具有“尾巴”特征的数据。

总之，指数函数在各个领域都有广泛的应用，可以帮助我们理解和解决各种实际问题和数学问题。

三、指数函数的运算法则公式14个

1、同底数相加减：对于两个底数相同的指数函数，可以将底数保持不变，同时将指数进行加减运算。例如，如果有两个指数函数f(x)=a^x和g(x)=a^y，其中a为常数，那么f(x)+g(x)=a^x+a^y，f(x)-g(x)=a^x-a^y。

2、同底数相乘：对于两个底数相同的指数函数，可以将底数保持不变，同时将指数相加。例如，如果有两个指数函数f(x)=a^x和g(x)=a^y，那么f(x)·g(x)=a^x·a^y=a^(x+y)。

3、同底数相除：对于两个底数相同的指数函数，可以将底数保持不变，同时将指数相减。例如，如果有两个指数函数f(x)=a^x和g(x)=a^y，那么f(x)/g(x)=a^x/a^y=a^(x-y)。

4、幂函数的乘积：对于两个幂函数，可以将底数相乘，同时将指数相加。例如，如果有两个幂函数f(x)=a^x和g(x)=b^x，那么f(x)·g(x)=(a^x)·(b^x)=a^x·b^x=(ab)^x。

5、幂函数的除法：对于两个幂函数，可以将底数相除，同时将指数相减。例如，如果有两个幂函数f(x)=a^x和g(x)=b^x，那么f(x)/g(x)=(a^x)/(b^x)=a^x/b^x=(a/b)^x。

6、指数函数的乘方：对于一个指数函数的乘方，可以将底数相乘，同时将指数相乘。例如，如果有一个指数函数f(x)=a^x，那么f(x)^n=(a^x)^n=a^(x·n)。

7、幂函数的乘方：对于一个幂函数的乘方，可以将底数进行乘方，同时将指数进行乘法运算。例如，如果有一个幂函数f(x)=a^x，那么f(x)^n=(a^x)^n=a^(x·n)。

8、指数函数的复合函数：对于一个指数函数f(x)=a^x和一个基本函数g(x)，可以将指数函数作为基本函数的参数进行复合运算。例如，如果有一个基本函数g(x)=sinx，那么f(g(x))=a^(sinx)。

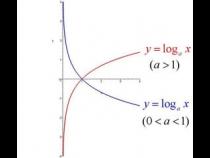
9、指数函数的反函数：指数函数的反函数是对数函数，可以将指数函数的结果作为对数函数的参数进行运算。例如，如果有一个指数函数f(x)=a^x，那么对数函数g(x)=log_a(x)就是f(x)的反函数。

10、指数函数的函数图像的平移：对于指数函数f(x)=a^x，如果对其进行平移，可以通过改变指数函数的底数和指数来实现。例如，f(x)=a^(x+h)表示将函数图像在x轴方向平移h个单位，f(x)=a^(x-k)表示将函数图像在y轴方向平移k个单位。

11、指数函数的函数图像的伸缩：对于指数函数f(x)=a^x，如果对其进行伸缩，可以通过改变指数函数的底数和指数来实现。例如，f(x)=a^(b·x)表示将函数图像在x轴方向上压缩或拉伸，f(x)=c·a^x表示将函数图像在y轴方向上压缩或拉伸。

12、指数函数的对数函数的性质：对于一个指数函数f(x)=a^x，其对数函数g(x)=log_a(x)具有以下性质：g(f(x))=x和f(g(x))=x。

13、指数函数的导数：指数函数的导数等于该指数函数的值乘以该指数的自然对数e。例如，对于指数函数f(x)=a^x，其导数为f'(x)=a^x·ln(a)。

14、复合指数函数的导数：复合指数函数的导数可以通过链式法则来计算。例如，对于复合指数函数f(x)=a^(g(x))，其导数为f'(x)=a^(g(x))·g'(x)·ln(a)。

1、复利计算：复利是指将利息加到本金中，下一个计息周期将利息计算到新的本金上。复利公式即为指数函数的应用。

2、人口增长：人口增长通常用指数函数来描述，底数a表示人口增长的速率。

3、感染病例统计：传染病的蔓延过程可以用指数函数来描述，底数a表示感染的速率。

4、放射性衰变：放射性元素的衰变常用指数函数来描述，底数a表示衰变的速率。