什么是指数函数,什么是对数函数

发布时间:2025-05-20 13:15:47 发布人:远客网络

什么是指数函数,什么是对数函数

一、什么是指数函数,什么是对数函数

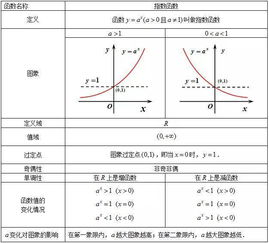
1、指数函数是重要的基本初等函数之一。一般地，y=aˣ函数(a为常数且以a>0，a≠1)叫做指数函数，函数的定义域是 R。注意，在指数函数的定义表达式中，在aˣ前的系数必须是数1，自变量x必须在指数的位置上，且不能是x的其他表达式，否则，就不是指数函数。

2、一般地，如果a（a大于0，且a不等于1）的b次幂等于N(N>0)，那么数b叫做以a为底N的对数，记作log aN=b,读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。一般地，函数y=log(a)X，（其中a是常数，a>0且a不等于1）叫做对数函数，它实际上就是指数函数的反函数，可表示为x=a^y。因此指数函数里对于a的规定，同样适用于对数函数。

二、什么是指数函数,什么是幂函数

区别方法：观察函数的自变量 x所在的位置，x在指数位置就是指数函数，x在底数位置就是幂函数。

-----------------------------------------------------------------------------

形如 y=a^x(a>0且a≠1)(x∈R)的函数叫指数函数。

a>1时指数函数 y=a^x是增函数

0<a<1时指数函数 y=a^x是减函数

-----------------------------------------------------------------------------

形如 y=x^α(α为常数）的函数叫幂函数。即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。例如函数y=x^0、y=x^1、y=x^2、y=x^(-1)（注：y=x^(-1)=1/x, y=x^0时 x≠0）等都是幂函数。当α取非零的有理数时是比较容易理解的，而对于α取无理数时，不大容易理解。因此，在初等函数里，不要求掌握指数为无理数的问题，只需接受它作为一个已知事实即可，因为这涉及到实数连续性的极为深刻的知识。

幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看其奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．

当α>0时，幂函数 y=x^α有下列性质：

a、图像都经过点（1,1）(0,0）；

b、函数的图像在区间 [0,+∞)上是增函数；

c、在第一象限内，α>1时，导数值逐渐增大；α=1时，导数为常数；0<α<1时，导数值逐渐减小，趋近于0；

a=2时即为二次函数 y=x²（抛物线）

当α<0时，幂函数 y=x^α有下列性质：

b、图像在区间（0，+∞）上是减函数；若为x^(-2)，易得到其为偶函数。利用对称性，对称轴是y轴，可得其图像在区间（-∞，0）上单调递增。其余偶函数亦是如此。

c、在第一象限内，有两条渐近线（即坐标轴），自变量趋近0，函数值趋近+∞，自变量趋近+∞，函数值趋近0。

a=-1时即为反比例函数 y=1/x（双曲线）

当α=0时，幂函数 y=x^a有下列性质：

y=x^0的图像是直线y=1去掉一点（0,1），是两条射线，不是连续的直线（即中间有空洞）。