回文数详细资料大全

一、回文数详细资料大全

“回文”是指正读反读都能读通的句子，它是古今中外都有的一种修辞方式和文字游戏，如“我为人人，人人为我”等。在数学中也有这样一类数字有这样的特征，成为回文数（palindrome number）。

设n是一任意自然数。若将n的各位数字反向排列所得自然数n1与n相等，则称n为一回文数。例如，若n=1234321，则称n为一回文数；但若n=1234567，则n不是回文数。

1.偶数个的数字也有回文数124421

二、什么是回文数

1、“回文”是指正读反读都能读通的句子，它是古今中外都有的一种修辞方式和文字游戏，如“我为人人，人人为我”等。在数学中也有这样一类数字有这样的特征，成为回文数（palindrome number）。

2、设n是一任意自然数。若将n的各位数字反向排列所得自然数n1与n相等，则称n为一回文数。例如，若n=1234321，则称n为一回文数；但若n=1234567，则n不是回文数。

3、回文数算法：随意找一个十进制的数，把它倒过来成另一个数，再把这两个数相加，得一个和数，这是第一步;然后把这个和数倒过来，与原来的和数相加，又得到一个新的和数，这是第二步。

4、照此方法，一步步接续往下算，直到出现一个“回文数”为n。例如:28+82=110,110+011=121，两步就得出了一个“回文数”。如果接着算下去，还会得到更多的“回文数”。这个过程称为“196算法”。

三、回文数简介

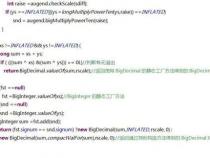
1、在JAVA编程中，有一个名为Plalindrome的类，用于判断数字是否为回文数。如测试示例所示：

2、11是回文数，因为 isPlalindrome(11)返回 true。

3、123不是回文数，isPlalindrome(123)返回 false。

4、17251也不是回文数，isPlalindrome(17251)返回 false。

5、2882是回文数，isPlalindrome(2882)返回 true。

6、有趣的是，有些数通过特定方式相加可以得到回文数，例如 29+92=121和 194+491=685。这种现象在某些算式中更为明显，比如：

7、3×51=153, 6×21=126, 4307×62=267034, 9×7×533=33579

8、这些被称为“回文算式”，它们的乘积在去掉乘号和等号后仍然是回文。此外，还有特殊的回文算式，如 12×231=132×21和 12×4032=2304×21，它们的乘积也是回文。

9、对于四位和六位的回文数，有明显的规律，如四位回文数1000a+100b+b10+a总是能被11整除。至于回文数在完全平方数和立方数中的比例，显然比一般自然数大。

10、然而，关于五次方或更高次幂的回文数，至今尚未发现。数学家们猜测可能不存在这种形式的回文数。此外，虽然电子计算器实验发现自然数与倒序数的反复相加会最终得到回文数，但对于特定的数如196，这个过程可能需要无限次步骤，具体步数无法确定。

11、"回文数"是一种数字。如：98789,这个数字正读是98789,倒读也是98789,正读倒读一样，所以这个数字就是回文数。