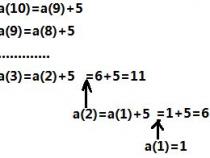python解决汉诺塔问题

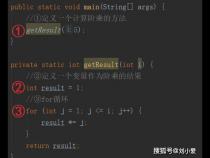
一、python解决汉诺塔问题

1、类似如何将大象装进冰箱：1）将冰箱门打开；2）把大大象放进去；3）把冰箱门关上……

2、我们将所有的盘都在同一个杆上从大到小排列视为【完美状态】，那么，目标就是将最大盘片为n的完美状态从a杆移到b杆，套用装大象的思路，这个问题同样是三步：

3、1）把n-1的完美状态移到另一个杆上；

4、3）把n-1的完美状态移到目标杆上。

二、汉诺塔python输出移动了多少次

导读：今天首席CTO笔记来给各位分享关于汉诺塔python输出移动了多少次的相关内容，如果能碰巧解决你现在面临的问题，别忘了关注本站，现在开始吧！

move(n,A,B)就表示把第n个饼从A柱移到B柱，其中step是个全局变量，用来记录移动的次数。

hanoi(n,A,B,C)就是你所问的实现递归的函数，表示把n个饼从A柱通过B柱移到C柱。

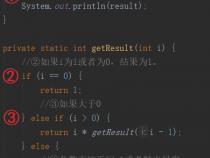
其中n==1是递归的最基本的情况，如果只有一个饼就直接移到目标柱子即可。

不然呢我们就先把最上面n-1个饼从A通过C移到B，注意这里移到的是B柱哦~，然后把第n块饼移到C柱，再重新把之前移到B柱上的n-1个饼通过A移动到C。

整个过程挺直白的，想通了就明白了

c++汉诺塔怎么输出每次移动是第几次移动？

我使用了一个全局变量count来计量次数：

我使用了一个全局变量count来计量次数：

void?hanoi(int?d,?char?from,?char?to,?char?others);

void?hanoi(int?d,?char?from,?char?to,?char?others)

????????printf("Number?%d?action:?%c----%c.\n",?count,?from,?to);

????hanoi(d?-?1,?from,?others,?to);

????hanoi(1,?from,?to,?others);

????hanoi(d?-?1,?others,?to,?from);

全局变量是无论在主函数还是子函数都能读取，修改的变量

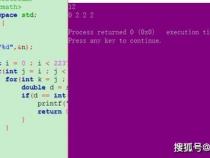
假设有n个圆盘，移动次数为f(n),根据经验，f(1)=1,f(2)=3

以3层为例，进行推导。可把整个过程分成三步，其中三个圆盘分别用A、B、C、代替且A的半径B的半径C的半径

1、把A、B移到中间的柱子，需要f(2)步

2、把C移动到第三根柱子，需要1步

3、把A、B再移动到第三根柱子，需要f(2)步

同理，当圆盘数量为4时，三个步骤分别需要f(3)步、1步、f(3)步，即f(4)=f(3)+1+f(3)=15

由此可得递推公式：f(x+1)=2*f(x)+1

进一步可以通项公式：f(x)=2^x-1

方案2：交互模式(建立函数文件jichu.py，在交互窗口调用文件中函数move)

????????print(a,'--',c,'\t%s'?%?s)

printf("请输入汉诺塔的金片数:");

voidhanoi(intn,inta,intb,intc,intstep);

voidhanoi(intn,inta,intb,intc,intstep)

结语：以上就是首席CTO笔记为大家整理的关于汉诺塔python输出移动了多少次的全部内容了，感谢您花时间阅读本站内容，希望对您有所帮助，更多关于汉诺塔python输出移动了多少次的相关内容别忘了在本站进行查找喔。

三、文科生快速入门python(十二) | 经典的函数递归案例

文科生快速入门Python中经典的函数递归案例，主要包括以下内容：

1.阶乘的递归计算定义：阶乘通常定义为n的阶乘等于n乘以的阶乘，直到n为1时停止递归。递归实现：通过递归函数，可以很方便地计算阶乘。递归函数会不断调用自身，直到达到基准情况，然后逐层返回结果。

2.汉诺塔问题的递归解决问题描述：汉诺塔问题是一个经典的递归问题，需要将一个柱子上的圆盘按规则逐步移动到另一柱子。递归策略：递归解决汉诺塔问题的策略是将问题分解为更小的子问题。首先假设已成功移动n1个圆盘，然后将最下面的圆盘移到目标柱子，再将剩余的n1个圆盘按照相同方式移动到目标柱子，最后将最下面的圆盘放回原处。代码实现：递归函数的参数通常包括圆盘数量、起始柱子、目标柱子和辅助柱子。通过递归调用，可以逐步解决整个问题。

总结：递归是Python编程中一个强大的工具，特别适合解决那些可以分解为更小相似问题的问题。通过理解和实践递归，文科生可以更好地掌握Python编程，提高解决问题的能力。

如果对递归或其他Python主题有更多疑问或兴趣，建议查阅相关资料或咨询专业人士。