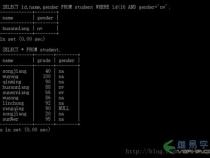
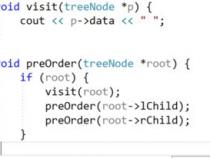
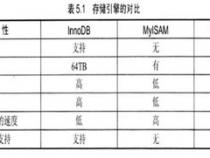
学习Python元组,有哪些必须要掌握的内容

一、学习Python元组,有哪些必须要掌握的内容

学习Python元组，有哪些必须要掌握的内容？

元组是Python的一种内建数据结构。关于元组：

1、元组属于序列，可以存放任意元素（任意类型对象），且有序（前后位置关系）。

2、元组支持整数索引访问其中的数据，也支持切片。

3、元组和列表不同是，元组不可变，列表可变。

元组不可变，某些操作比列表高效。

使用()可以创建元组，元组元素间使用”,”分隔，元组内部元素可以是任意元素，也可以是元组。

元组不可变除了不能修改，也不能删除元组元素，但删除与元组绑定的变量是没问题的。

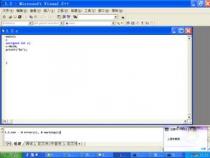
使用（）方式创建只有一个元素的元组时要注意，因为一个元素使用()括起来，表示元素本身，如100，（100），两者等价，如果创建只包含100的元组应该使用：(100,)方式。

图：使用（）创建只有一个元素的元组

使用构造函数tuple()创建元组。了解更多信息可以使用help(tuple)来查看具体帮助内容。

1、tuple()如果没有参数创建一个空元组。

2、tuple(可迭代对象)由可迭代对象创建一个元组，如字符串，列表。如果参数是元组将返回该元组。

和字符串列表一样，元组支持使用整数索引（下标方式访问），也支持切片方式访问元组的元素。

下标索引如果是正整数则从0开始表示第一个元素，……最有一个元素用元组长度-1表示；如果使用负整数做下标，-1表示最后一个元素，-2表示倒数第二个元素，……负的长度表示第一个元素。

！！！需要注意的是下标索引不能越界！！！

常用内建函数len、max、min、sum、reversed可以操作元组，函数解释如下：

使用min，max，sum函数操作元组，元组元素类型能被函数接受才可以，否则将报异常等错误。

count返回元组中对应值的个数，index返回对应值的位置（索引）。

元组支持+连接，*复制运算，in/not in运算

字符串，元组，列表都属于Python的序列结构，序列具有很多相同的属性和操作方法，如：序列中的每个元素被分配一个序号（位置，也叫索引），序号（索引）从0开始，依次类推；序列都支持切片操作等等。

Python内置了多种序列结构:字符串、列表、元组、Unicode字符串、buffer对象、range对象。序列是Python中一种重要的数据结构，必须要掌握，也很容易掌握。

二、Python-元组

1、思考：如果想要存储多个数据，但是这些数据是不能修改的数据，怎么做？

2、答：列表？列表可以一次性存储多个数据，但是列表中的数据允许更改。

3、一个元组可以存储多个数据，元组内的数据是不能修改的。

4、元祖特点：定义元组使用小括号，且用逗号隔开每个数据，数据可以是不同的数据类型

5、注意:如果定义的元组只有一个数据,那么这个数据后必须添加逗号，否则数据类型为唯一的

6、元组数据不支持修改,只支持查找,具体如下:

三、python为什么引入元组的概念

python为什么引入元组的概念

元祖和序列是相对的，元祖是不可变的序列，一旦建立无法修改里面的值。

元祖和序列是相对的，元祖是不可变的序列，一旦建立无法修改里面的值。

建立形式1：用(.)。注意，最后要加多一个.

元组操作比较简单，记住其是不可变的

应力平衡压力与其机械载荷所必须向应力或剪应力应力三类：1．总体薄膜应力影响范围遍及整结构薄膜应力塑性流程总体薄膜应力重新布直接导致结构破坏2．区域性薄膜应力应力水平于总体薄膜应力影响范围仅限于结构区域性区域薄膜应力结构局部发塑性流类应力重新布若加限制则载荷结构某高应力区传递另低应力区产量塑性变形导致破坏3.弯曲应力平衡压力或其机械载荷所需沿截面厚度线性布弯曲应力二应力满足外部约束条件或结构自身变形连续要求所须向应力或剪应力二应力基本特征具自限性即区域性屈服量变形使约束条件或变形连续要求满足变形再继续增要反复载入二应力导致结构破坏峰值应力由区域性结构连续或区域性热应力影响引起附加加二应力应力增量

就是说，有理数加减乘除是出不了无理数的。只有无限次的加减乘除才可能把有理数变为无理数（实数系的完备性）。无限次的加减乘除不可能把有理数变为复数。以后线代还有开方运算，出了虚数，所以研究数域是很重要的。

简单点就是一个域名的目的是便于记忆和沟通的一组伺服器的地址，因为IP地址是Inter主机的作为路由定址用的数字型标识，人不容易记忆。因而产生了域名（domain name）这一种字元型标识。

希望可以帮助到你，如有疑问请追问，满意请采纳！

应力是由于他的存在才有它的概念，比如内应力是指物件内部所受的力，当你想通过外力改变它的形状，他的内部就回有个力个你抵抗。就像以前打铁造工具那样，必须烧红，消除它的应力，它才可能由一块铁变成你想要的形状。要是不烧红消除它的应力，那块铁当受力到一定的程度就会折断。

修正久期指的是对于给定的到期收益率的微小变动，债券价格的相对变动与其麦考利久期为正变关系。这种正变关系只是一种近似的比例关系，它的成立是以债券的到期收益率很小为前提的。当然，为了更精确地描述债券价格对于到期收益率变动的灵敏性，又引入了修正久期模型（ModifiedDurationModel）,考虑凸度。

人在路面上用绳子拉一个物体,绳子上的力F与路面成的角为θ,物体产生的位移为S,则F对物体作的功为

我们可把功作为力F和位移S的数量积,即; W=F·S

偏摩尔量的定义：在温度、压力及除了组分B以外其余组分的物质的量均不变的条件下,广度量X随组分B的物质的量nB变化率XB称为组分B的偏摩尔量。

对于纯物质,并不存在偏摩尔量的概念，它就是摩尔量。

偏摩尔体积可以看作是某一定浓度溶液中1摩尔该组分体系总体积的贡献。

一是通过偏摩尔量的集合公式，利用各组分的偏摩尔量，可求得体系总的热力学函式。

二是化学势（偏摩尔吉布斯自由能）是物质平衡的重要判据，其本身是一个偏摩尔量。

偏摩尔量的提出，主要是为了解决多组分单相热力学的问题。