详解C语言用数组表示杨辉三角...

发布时间:2025-05-12 18:40:21 发布人:远客网络

详解C语言用数组表示杨辉三角...

一、详解C语言用数组表示杨辉三角...

的三角形，其实质是二项式(a+b)的n次方展开后各项的系数排成的三角形，它的特点是左右两边全是1，从第二行起，中间的每一个数是上一行里相邻两个数之和。这个题目常用于程序设计的练习。

{ printf("请输入杨辉三角形的行数:");

a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/

for(i=0;i<n;i++)/*输出杨辉三角*/

点评：解法一是一般最容易想到的解法，各部分功能独立，程序浅显易懂。

{ printf("请输入杨辉三角形的行数:");

{ a[i][0]=1;/*第一列全置为一*/

a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/

for(i=0;i<n;i++)/*输出杨辉三角*/

点评：解窢二是在解法一的基础上，把第一列置为1的命令移到下面的双重循环中，减少了一个循环。注意初始化数组的变化。

{ int i,j,n=0,a[17][17]={0,1};

{ printf("请输入杨辉三角形的行数:");

a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/

for(i=1;i<=n;i++)/*输出杨辉三角*/

{ for(j=1;j<=i;j++) printf("%5d",a[i][j]);

点评：解法三是在解法一、二的基础上，把第一列置为1的命令去掉了，注意初始化数组的变化。

{ int i,j,n=0,a[17][17]={0,1};

{ printf("请输入杨辉三角形的行数:");

{ a[i][j]=a[i-1][j-1]+a[i-1][j];/*每个数是上面两数之和*/

printf("%5d",a[i][j]);/*输出杨辉三角*/

点评：解法四是在解法三的基础上，把计算和打印合并在一个双重循环中。

{ int i,j,n=0,a[17]={1},b[17];

{ printf("请输入杨辉三角形的行数:");

b[j]=a[j-1]+a[j];/*每个数是上面两数之和*/

for(j=0;j<=i;j++)/*输出杨辉三角*/

{ a[j]=b[j];/*把算得的新行赋给a,用于打印和下一次计算*/

点评：解法一到解法四都用了二维数组，占用的空间较多。而解法五只使用了两个一维数组。

{ int i,j,n=0,a[17]={0,1},l,r;

{ printf("请输入杨辉三角形的行数:");

a[j]=l+r;/*每个数是上面两数之和*/

printf("%5d",a[j]);/*输出杨辉三角*/

点评：解法六只使用了一个一维数组和两个临时变量。

二、如何用C语言打印杨辉三角前10行

杨辉三角是一种数学图形，它是由中国古代数学家杨辉所发明的，因此得名为杨辉三角。它是一个三角形，其中的每个数字都是由上面的两个数字相加而来的。杨辉三角在数学中有着广泛的应用，尤其是在组合数学和概率论中。在本文中，我们将使用C语言编写程序来输出杨辉三角的前10行。

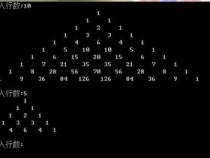
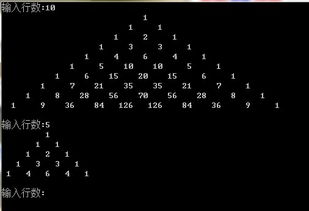
让我们来了解一下杨辉三角的规律。杨辉三角的第一行只有一个数字1，第二行有两个数字1，第三行有三个数字1，以此类推。每行的两端都是1，中间的数字是由上一行相邻的两个数字相加而来的。例如，第三行的中间数字是2，它是由第二行的两个数字1相加而来的。下面是杨辉三角的前10行:

第一行：1、1；第二行：1、2、1；第三行：1、3、3、1；第四行：1、4、6、4、1；第五行：1、5、10、10、51；第六行：1、6、15、20、15、6、1；第七行：1、7、21、35、35、21、7、1；第八行：1、8、28、56、70、56、28、8、1；第九行：1、9、36、84、126、126、84、36、9、1。

C语言是一门面向过程的、抽象化的通用程序设计语言，广泛应用于底层开发。C语言能以简易的方式编译、处理低级存储器。C语言是仅产生少量的机器语言以及不需要任何运行环境支持便能运行的高效率程序设计语言。

尽管C语言提供了许多低级处理的功能，但仍然保持着跨平台的特性，以一个标准规格写出的C语言程序可在包括类似嵌入式处理器以及超级计算机等作业平台的许多计算机平台上进行编译。