c语言常用算法有哪些

一、c语言常用算法有哪些

1、穷举法简单粗暴，没有什么问题是搞不定的，只要你肯花时间。同时对于小数据量，穷举法就是最优秀的算法。就像太祖长拳，简单，人人都能会，能解决问题，但是与真正的高手过招，就颓了。

2、贪婪算法可以获取到问题的局部最优解，不一定能获取到全局最优解，同时获取最优解的好坏要看贪婪策略的选择。特点就是简单，能获取到局部最优解。就像打狗棍法，同一套棍法，洪七公和鲁有脚的水平就差太多了，因此同样是贪婪算法，不同的贪婪策略会导致得到差异非常大的结果。

3、当最优化问题具有重复子问题和最优子结构的时候，就是动态规划出场的时候了。动态规划算法的核心就是提供了一个memory来缓存重复子问题的结果，避免了递归的过程中的大量的重复计算。动态规划算法的难点在于怎么将问题转化为能够利用动态规划算法来解决。当重复子问题的数目比较小时，动态规划的效果也会很差。如果问题存在大量的重复子问题的话，那么动态规划对于效率的提高是非常恐怖的。就像斗转星移武功，对手强它也会比较强，对手若，他也会比较弱。

4、分治算法的逻辑更简单了，就是一个词，分而治之。分治算法就是把一个大的问题分为若干个子问题，然后在子问题继续向下分，一直到base cases，通过base cases的解决，一步步向上，最终解决最初的大问题。分治算法是递归的典型应用。

5、回溯算法是深度优先策略的典型应用，回溯算法就是沿着一条路向下走，如果此路不同了，则回溯到上一个

6、分岔路，在选一条路走，一直这样递归下去，直到遍历万所有的路径。八皇后问题是回溯算法的一个经典问题，还有一个经典的应用场景就是迷宫问题。

7、回溯算法是深度优先，那么分支限界法就是广度优先的一个经典的例子。回溯法一般来说是遍历整个解空间，获取问题的所有解，而分支限界法则是获取一个解（一般来说要获取最优解）。

二、C语言常用算法有哪些最好能具体的举出来

1、C语言中的算法种类繁多，包括递归、回溯、排序、查找、穷举、贪心、分治、深度搜索、广度搜索、动态规划和拓扑排序等。这些算法各自独立，适用于不同的问题场景。递归算法通过将问题分解为更小的子问题来解决问题，回溯算法常用于寻找所有可能的解，排序算法则用于将数据按照特定顺序排列，查找算法用于在数据结构中定位特定元素，穷举算法适用于尝试所有可能解，贪心算法在每一步都选择最优解，分治算法将问题分解为多个子问题，深度搜索和广度搜索用于图或树的遍历，动态规划通过将问题分解为子问题并存储结果来提高效率，拓扑排序用于有向无环图的排序。

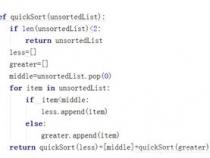
2、以排序算法为例，常见的有冒泡排序、插入排序、选择排序、快速排序、归并排序和堆排序等。冒泡排序通过相邻元素比较交换实现排序，插入排序将数组分成已排序和未排序两部分，将未排序部分的第一个元素插入到已排序部分的适当位置，选择排序每次从未排序部分选择最小的元素放到已排序部分的末尾，快速排序通过选取基准值将数组分为两部分，递归地对这两部分进行排序，归并排序通过将数组不断分割，再将已排序的子数组合并，堆排序利用大顶堆或小顶堆实现排序。这些算法各有优缺点，适用场景也不同。

3、贪心算法则是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。例如，贪心算法在图的最小生成树问题中，每次选择当前边权最小的边加入最小生成树，直到所有顶点都在最小生成树中。贪心算法在某些问题上可以快速找到最优解，但在其他问题上则可能无法保证最优解。

4、分治算法将一个复杂的问题分解为两个或更多的相同或相似的子问题，然后递归地求解这些子问题。例如，在归并排序中，将数组不断分割为更小的部分，直到每个部分只有一个元素，然后合并这些部分。分治算法通过将大问题分解为小问题，可以有效地解决问题，但需要确保子问题的解可以合并为原问题的解。

5、深度搜索和广度搜索都是图或树的遍历算法。深度搜索从根节点开始，优先访问节点的子节点，直到无法访问为止，再回溯到父节点继续访问其子节点，直到所有节点都被访问。广度搜索则从根节点开始，优先访问与当前节点相邻的节点，直到所有节点都被访问。深度搜索和广度搜索在不同的场景下有着各自的优势和劣势。

6、动态规划算法通过将问题分解为子问题，并存储子问题的解来避免重复计算，从而提高效率。例如，在背包问题中，通过将物品分成更小的部分，递归地计算每种物品的选择方案，最终得到最优解。动态规划算法适用于具有最优子结构和重叠子问题的问题，但需要确保子问题的解可以合并为原问题的解。

三、C语言算法有哪些 并举例和分析

function gcd(a,b:integer):integer;

function lcm(a,b:integer):integer;

while lcm mod b>0 do inc(lcm,a);

A.小范围内判断一个数是否为质数：

function prime(n: integer): Boolean;

B.判断longint范围内的数是否为素数（包含求50000以内的素数表）：

function prime(x:longint):integer;

else if x mod pr[i]=0 then exit;

lowcost,closest:array[1..maxn] of integer;

{寻找离生成树最近的未加入顶点k}

if(lowcost[j]<min) and(lowcost[j]<>0) then begin

lowcost[k]:=0;{将顶点k加入生成树}

{生成树中增加一条新的边k到closest[k]}

{修正各点的lowcost和closest值}

if cost[k,j]<lwocost[j] then begin

按权值递增顺序删去图中的边，若不形成回路则将此边加入最小生成树。

function find(v:integer):integer;{返回顶点v所在的集合}

while(i<=n) and(not v in vset[i]) do inc(i);

if i<=n then find:=i else find:=0;

for i:=1 to n do vset[i]:=[i];{初始化定义n个集合，第I个集合包含一个元素I}

p:=n-1; q:=1; tot:=0;{p为尚待加入的边数，q为边集指针}

{对所有边按权值递增排序，存于e[I]中，e[I].v1与e[I].v2为边I所连接的两个顶点的序号，e[I].len为第I条边的长度}

i:=find(e[q].v1);j:=find(e[q].v2);

vset[i]:=vset[i]+vset[j];vset[j]:=[];

a:array[1..maxn,1..maxn] of integer;

b:array[1..maxn] of integer;{b[i]指顶点i到源点的最短路径}

mark:array[1..maxn] of boolean;

fillchar(mark,sizeof(mark),false);

mark[1]:=true; b[1]:=0;{1为源点}

If mark[i] then{对每一个已计算出最短路径的点}

if(not mark[j]) and(a[i,j]>0) then

if(best=0) or(b[i]+a[i,j]<best) then begin

b[best_j]:=best；mark[best_j]:=true;

B.Floyed算法求解所有顶点对之间的最短路径：

if a[I,j]>0 then p[I,j]:=I else p[I,j]:=0;{p[I,j]表示I到j的最短路径上j的前驱结点}

for k:=1 to n do{枚举中间结点}

if a[i,k]+a[j,k]<a[i,j] then begin

a:array[1..maxn,1..maxn] of integer;

b,pre:array[1..maxn] of integer;{pre[i]指最短路径上I的前驱结点}

mark:array[1..maxn] of boolean;

procedure dijkstra(v0:integer);

fillchar(mark,sizeof(mark),false);

if d[i]<>0 then pre[i]:=v0 else pre[i]:=0;

repeat{每循环一次加入一个离1集合最近的结点并调整其他结点的参数}

min:=maxint; u:=0;{u记录离1集合最近的结点}

if(not mark[i]) and(d[i]<min) then begin

if(not mark[i]) and(a[u,i]+d[u]<d[i]) then begin

T:array[1..maxn,1..maxn] of boolean;

For j:=1 to n do T[I,j]:=t[I,j] or(t[I,k] and t[k,j]);

procedure dfs( now,color: integer);

if a[now,i] and c[i]=0 then begin{对结点I染色}

几个定义：顶点1为源点，n为汇点。

a.顶点事件最早发生时间Ve[j], Ve [j]= max{ Ve [j]+ w[I,j]},其中Ve(1)= 0;

b.顶点事件最晚发生时间 Vl[j], Vl [j]= min{ Vl[j]– w[I,j]},其中 Vl(n)= Ve(n);

c.边活动最早开始时间 Ee[I],若边I由<j,k>表示，则Ee[I]= Ve[j];

d.边活动最晚开始时间 El[I],若边I由<j,k>表示，则El[I]= Vl[k]– w[j,k];

若 Ee[j]= El[j]，则活动j为关键活动，由关键活动组成的路径为关键路径。

a.从源点起topsort,判断是否有回路并计算Ve;

找入度为0的点，删去与其相连的所有边，不断重复这一过程。

例寻找一数列，其中任意连续p项之和为正，任意q项之和为负，若不存在则输出NO.

定义：经过图的每条边仅一次的回路。（充要条件：图连同且无奇点）

定义：经过图的每个顶点仅一次的回路。

充要条件：图连通且奇点个数为0个或2个。

9．判断图中是否有负权回路 Bellman-ford算法

x[I],y[I],t[I]分别表示第I条边的起点，终点和权。共n个结点和m条边。

for I:=0 to n-1 do d[I]:=+infinitive;

for j:=1 to m do{枚举每一条边}

if d[x[j]]+t[j]<d[y[j]] then d[y[j]]:=d[x[j]]+t[j];

if d[x[j]]+t[j]<d[y[j]] then return false else return true;

*第二最短路径：每举最短路径上的每条边，每次删除一条，然后求新图的最短路径，取这些路径中最短的一条即为第二最短路径。

*同理，第n最短路径可在求解第n-1最短路径的基础上求解。

*部分背包问题可有贪心法求解：计算Pi/Wi

1．0-1背包：每个背包只能使用一次或有限次(可转化为一次)：

有一个箱子容量为v(正整数，o≤v≤20000)，同时有n个物品(o≤n≤30)，每个物品有一个体积(正整数)。要求从 n个物品中，任取若千个装入箱内，使箱子的剩余空间为最小。

procedure search(k,v:integer);{搜索第k个物品，剩余空间为v}

if v-(s[n]-s[k-1])>=best then exit;{s[n]为前n个物品的重量和}

if v>w[k] then search(k+1,v-w[k]);

F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志，为布尔型。

实现:将最优化问题转化为判定性问题

f [I, j]= f [ i-1, j-w[i] ](w[I]<=j<=v)边界：f[0,0]:=true.

For j:=w[I] to v do F[I,j]:=f[I-1,j-w[I]];

优化：当前状态只与前一阶段状态有关，可降至一维。

If f[j-w[I]] then f1[j]:=true;

F[I,j]为容量为I时取前j个背包所能获得的最大价值。

F [i,j]= max{ f [ i– w [ j ], j-1]+ p [ j ], f[ i,j-1]}

if j+now<=n then inc(c[j+now],a[j]);

F[I,j]为前i个物品中选择若干个放入使其体积正好为j的标志，为布尔型。

f[I,j]= f [ I-1, j– w[I]*k ](k=1.. j div w[I])

进行一次竞赛，总时间T固定，有若干种可选择的题目，每种题目可选入的数量不限，每种题目有一个ti（解答此题所需的时间）和一个si（解答此题所得的分数），现要选择若干题目，使解这些题的总时间在T以内的前提下，所得的总分最大，求最大的得分。

f[i,j]= max{ f [i- k*w[j], j-1]+ k*p[j]}(0<=k<= i div w[j])

其中f[i,j]表示容量为i时取前j种背包所能达到的最大值。

If i-problem[j].time>=0 Then

t:=problem[j].point+f[i-problem[j].time];

求自然数n本质不同的质数和的表达式的数目。

思路一，生成每个质数的系数的排列，在一一测试，这是通法。

cal;{此过程计算当前系数的计算结果，now为结果}

if dep=l+1 then begin{生成所有系数}

for i:=0 to n div pr[dep] do begin

procedure try(dep,rest:integer);

if(rest<=0) or(dep=l+1) then begin

for i:=0 to rest div pr[dep] do

V个物品，背包容量为n，求放法总数。

if j+now*k<=n then inc(c[j+now*k],a[j]);

read(now);{读入第一个物品的重量}

i:=0;{a[i]为背包容量为i时的放法总数}

a[i]:=1; inc(i,now); end;{定义第一个物品重的整数倍的重量a值为1，作为初值}

i:=l;j:=r; mid:=a[(l+r) div 2];{将当前序列在中间位置的数定义为中间数}

while a[i]<mid do inc(i);{在左半部分寻找比中间数大的数}

while a[j]>mid do dec(j);{在右半部分寻找比中间数小的数}

if i<=j then begin{若找到一组与排序目标不一致的数对则交换它们}

if l<j then qsort(l,j);{若未到两个数的边界，则递归搜索左右区间}

思路：当前a[1]..a[i-1]已排好序了，现要插入a[i]使a[1]..a[i]有序。

if a[i]>a[j] then swap(a[i],a[j]);

if a[j]<a[j-1] then swap( a[j],a[j-1]);{每次比较相邻元素的关系}

procedure sift(i,m:integer);{调整以i为根的子树成为堆,m为结点总数}

a[0]:=a[i]; k:=2*i;{在完全二叉树中结点i的左孩子为2*i,右孩子为2*i+1}

if(k<m) and(a[k]<a[k+1]) then inc(k);{找出a[k]与a[k+1]中较大值}

if a[0]<a[k] then begin a[i]:=a[k];i:=k;k:=2*i; end

a[i]:=a[0];{将根放在合适的位置}

for j:=n div 2 downto 1 do sift(j,n);