汉诺塔c语言算法。注意是算法

一、汉诺塔c语言算法。注意是算法

我以前收藏了一个别人的回答，你看看吧：

递归算法的出发点不是由初始条件出发，而是把出发点放在求解的目标上，从所求的未知项出发逐次调用本身的求解过程，直到递归的边界（即初始条件）。

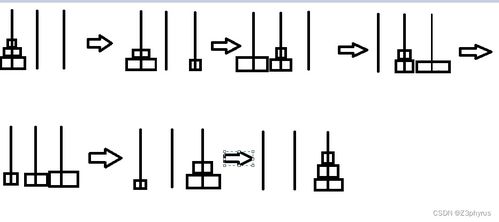
汉诺塔问题的重点是分析移动的规则，找到规律和边界条件。

若需要将n个盘子从A移动到C就需要（1）将n-1个盘子从A移动到B；（2）将你第n个从A移动到C；（3）将n-1个盘子再从B移动到C，这样就可以完成了。如果n!=1，则需要递归调用函数，将A上的其他盘子按照以上的三步继续移动，直到达到边界条件n=1为止。

思路清楚了，程序就好理解了。程序中的关键是分析好每次调用移动函数时具体的参数和对应的A、B、C塔的对应的关系。下面来以实际的例子对照程序进行说明。

①move(int n,int x,int y,int z)

④ printf("%c-->%c\n",x,z);

⑧ printf("%c-->%c\n",x,z);

⑨{getchar();}//此句有必要用吗？感觉可以去掉的吧

比如有4个盘子，现在全部放在A塔上。盘子根据编号为1、2、3、4依次半径曾大。现在要将4个盘子移动到C上，并且是按原顺序罗列。首先我们考虑如何才可以将4号移动到C呢？就要以B为中介，首先将上面的三个移动到B。此步的操作也就是程序中的①开始调入move函数（首次调用记为一），当然现在的n=4，然后判断即③n！=1所以不执行④而是到⑤再次调用move函数（记为二）考虑如何将3个盘移动到B的方法。此处是递归的调用所以又一次回到①开始调入move函数，不过对应的参数发生了变化，因为这次要考虑的不是从A移动4个盘到C，而是要考虑从A如何移动移动3个盘到B。因为n=3，故不可以直接移动要借助C做中介，先考虑将两个移动到C的方法，故再一次到⑤再一次递归调用move函数（记为三）。同理两个盘还是不可以直接从A移动到C所以要以B为中介考虑将1个移动到B的过程。这次是以B为中介，移动到C为目的的。接下来再一次递归调用move函数（记为四），就是移动到B一个，可以直接进行。程序执行③④句，程序跳出最内一次的调用（即跳出第四次的调用）返回上一次（第三次），并且从第三次的调用move函数处继续向下进行即⑧，即将2号移动到了C，然后继续向下进行到

⑩，再将已经移到B上的哪一个移回C，这样返回第二次递归（以C为中介将3个盘移动到B的那次）。执行⑧，将第三个盘从A移动到B，然后进入⑩，这次的调用时因为是将C上的两个盘移到B以A为中介，所以还要再一次的递归调用，对应的参数传递要分析清楚，谁是原塔谁是目标塔，谁是中介塔。过程类似于上面的分析，这里不再重复论述了。

二、C语言汉诺塔程序

1、将以下内容全部复制到新建的源文件中：（本人自己写的，因为你那课本上的代码，没解释，书写不规范，很难理解清楚，所以我直接新写了一个完整的代码，附带详细说明）

2、//汉诺塔x层塔从A塔整体搬到C塔，中间临时B塔。

3、//x层塔是从大到小往上叠放。每次移动只能移动一层塔。并且在移动过程中必须保证小层在上边

4、//借助B塔可以将x层塔全部从A搬到C上，并且符合要求（在移动过程中大的那块在下边，小的那块在上边）

5、void tower(int x,char a,char b,char c);//声明函数

6、int x=5,a='A',b='B',c='C';//x表示有5层塔，具体要多少层自己修改这个值。abc分别表示ABC塔。

7、tower(x,a,b,c);//x层塔从a移动到c的全过程，主程序只有这条有效语句

8、//参数解析：x层塔放在a上，b是中间塔，c是目标塔。即x层塔要从a搬到c上。

9、//此函数实现x层塔从a整体转移到c上。以及这个过程是怎么搬的全部过程。

10、void tower(int x,char a,char b,char c)

11、if(x==1)printf("将%d从%c放到%c\n",x,a,c);//只有1层塔时，直接从a搬到c上。

12、else//不止1层塔，则先将x-1层塔从a按照规律搬到b上，再将最后一块从a搬到c上，最后再将b上的x-1层塔按照规律搬到c上。

13、tower(x-1,a,c,b);//先将x-1层塔从a按照规律搬到b上，注意参数b放在最后，因为放在最后的参数是准备搬过去的目标塔。

14、printf("将%d从%c放到%c\n",x,a,c);//将最后一块从a搬到c上

15、tower(x-1,b,a,c);//最后再将b上的x-1层塔按照规律搬到c上，注意参数b放在开头，因为x-1层是要从b上搬过去的。

三、如何做一个C语言编程的汉诺塔游戏要有源代码。

1、 printf("%c-->%c\n",x,y);

2、 void hanoi(int n,char one,char two,char three)

3、 printf("input the number of disks:");

4、 printf("the step to moving%3d diskes:\n",m);

5、 hanoi(m,'A','B','C');

6、其实算法非常简单，当盘子的个数为n时，移动的次数应等于2^n– 1（有兴趣的可以自己证明试试看）。后来一位美国学者发现一种出人意料的简单方法，只要轮流进行两步操作就可以了。首先把三根柱子按顺序排成品字型，把所有的圆盘按从大到小的顺序放在柱子A上，根据圆盘的数量确定柱子的排放顺序：若n为偶数，按顺时针方向依次摆放 A B C；

7、若n为奇数，按顺时针方向依次摆放 A C B。

8、（1）按顺时针方向把圆盘1从现在的柱子移动到下一根柱子，即当n为偶数时，若圆盘1在柱子A，则把它移动到B；若圆盘1在柱子B，则把它移动到C；若圆盘1在柱子C，则把它移动到A。

9、（2）接着，把另外两根柱子上可以移动的圆盘移动到新的柱子上。即把非空柱子上的圆盘移动到空柱子上，当两根柱子都非空时，移动较小的圆盘。这一步没有明确规定移动哪个圆盘，你可能以为会有多种可能性，其实不然，可实施的行动是唯一的。

10、（3）反复进行（1）（2）操作，最后就能按规定完成汉诺塔的移动。

11、所以结果非常简单，就是按照移动规则向一个方向移动金片：

12、如3阶汉诺塔的移动：A→C,A→B,C→B,A→C,B→A,B→C,A→C

13、汉诺塔问题也是程序设计中的经典递归问题，下面我们将给出递归和非递归的不同实现源代码。