Matlab相机标定总结

一、Matlab相机标定总结

0.  A4纸打印出来（或直接在手机上）并用尺子测量一个格的边长。

1.用想要标定的相机拍摄各种角度的照片。（我用的是电脑相机拍摄手机上的图片，手机上全屏的图片用尺子测量的是小格子的边长为7mm）,15到20张即可。

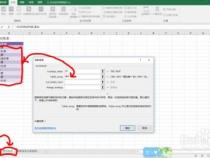
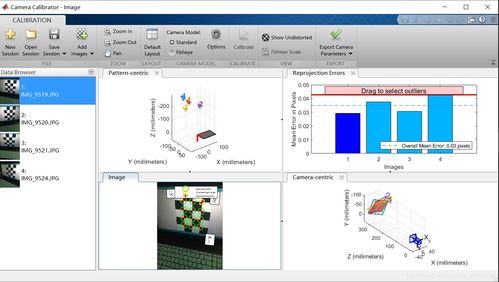
2.打开matlab命令行输入cameraCalibrator回车。点Add images，导入所拍的照片，改为7mm，确定。

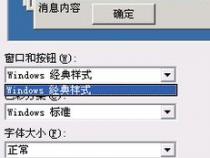
3.点击Options,勾选如图所示。点击Calibrate。

4,最后点击。Export Camera Parameters导出参数。

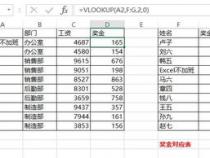
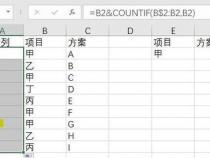
IntrinsicMatrix对应内参，注意这个和程序中是转置的关系，注意不要搞错。

RadiaDistortion即为相机的畸变矩阵对应k1，k2，k3。

TangentialDistortion对应p1，p2。

畸变参数，总共有五个，径向畸变3个（k1,k2,k3）和切向畸变2个(p1,p2)。

RotationMatrices为16张图片的外参矩阵translationVectors为16张图片的转移矩阵。因为每张图片对应一个世界坐标系（旋转矩阵和平移矩阵是世界坐标系相对于摄像机坐标系的，而算法中规定世界坐标系是标定板为z=0的平面，对于不同位置的标定板，其世界坐标系的定义是不同的，这也就不难解释为什么有多个旋转矩阵和平移矩阵了），所以实际情况时，内参矩阵，畸变矩阵确定后，选一个合适的世界坐标系，将其对应的外参矩阵和平移矩阵带入即可用于相机的坐标系转换。

二、matlab相机标定如何将像素坐标转换到世界坐标系下

1、布尔莎七参数模型在测绘领域广泛应用，适用于不同坐标系统间的转换，通过最小二乘法求解。MATLAB作为高效数据处理工具，以其简洁的编程方式受到欢迎。本文将利用MATLAB与布尔莎七参数模型，探讨WGS_84与XIAN_80坐标系统间的参数转换。如有不当之处，欢迎指正。

WGS_84坐标系为地心坐标系，坐标原点位于地球质心，z轴指向CTP方向，x轴指向零子午面与CTP赤道交点，y轴与xz轴构成右手坐标系，为世界大地坐标系统。XIAN_80坐标系为参心坐标系，坐标原点位于陕西省泾阳县永乐镇，x轴指向大地起始子午面内与z轴垂直，y轴与xz轴构成右手坐标系，为中国1980年设立的全国大地坐标系统。WGS_84与XIAN_80系统虽有差异，但其椭球参数较为接近。

七参数描述了两个坐标系统间的转换关系，包括坐标平移参数（dx, dy, dz）、坐标旋转参数（rx, ry, rz）及坐标尺度因子（m）。具体求解公式如下：

所谓七参数转换法，即布尔莎模型，旨在转换两个不同椭球之间相应点的坐标。最小二乘法被用于求解参数的最优化值，通常需要三个点的数据以确保解的稳定性。

转换流程主要包括以下几个步骤：

1.将三个点的坐标数据代入布尔莎方程组，产生九个方程。

2.根据最小二乘原理，将方程组整体平方并相加，形成一个总公式。

3.对参数求偏导，得到九个方程。

4.解算上述方程，获得七参数值。

MATLAB代码示例包括数据导入、偏导运算、参数求解等关键步骤，最终输出结果，便于分析。

通过MATLAB实现的代码，我们能够获取WGS_84与XIAN_80坐标系统间的七参数转换结果，并以表格形式展示。这一结果为坐标转换提供了精确的数据支持，对于大地测量、地图制作等领域具有重要应用价值。

三、关于matlab的应用

了解了 MATLAB的矩阵和向量概念与输入方法之后，MATLAB的二维绘图再简单也不过了。假设有两个同长度的向量 x和 y,则用 plot(x,y)就可以自动绘制画出二维图来。如果打开过图形窗口，则在最近打开的图形窗口上绘制此图，如果未打开窗口，则开一个新的窗口绘图。

>> t=0:.1:2*pi;%生成横坐标向量，使其为 0,0.1,0.2,...,6.2

这样立即可以得出如图所示的二维图 [4.1(a)]

plot()函数还可以同时绘制出多条曲线，其调用格式和前面不完全一致，但也好理解。

>> y1=cos(t); plot(t,y,t,y1);%或 plot(t,[y; y1]),即输出为两个行向量组成的矩阵。

plot()函数最完整的调用格式为：

>> plot(x1,y1,选项1, x2,y2,选项2, x3,y3,选项3,...)

其中所有的选项如表 4.1所示。一些选项可以连用，如'-r'表示红色实线。

由 MATLAB绘制的二维图形可以由下面的一些命令简单地修饰。如

>> xlabel('字符串')%给横坐标轴加说明

>> ylabel('字符串')%给纵坐标轴加说明，

>> title('字符串')%给整个图形加图题

axis()函数可以手动地设置 x,y坐标轴范围

还可以使用 plotyy()函数绘制具有两个纵坐标刻度的图形。

坐标系的分割在 MATLAB图形绘制中是很有特色的，比较规则的分割方式是用 subplot()函数定义的，其标准调用格式为

其中，n和 m为将图形窗口分成的行数和列数，而 k为相对的编号。例如在标准的 Bode图绘制中需要将窗口分为上下两个部分(即n=2, m=1),分割后上部编号为 1，下部编号为 2。

MATLAB的图形对象简介( 00-12-13)

MATLAB从 4.0版本开始就提出了句柄图形学(Handle Graphics)的概念,为面向对象的图形处理提供了十分有用的工具。和早期版本的 MATLAB相比较，其最大区别在于，它在图形绘制时其中每个图形元素

(比如其坐标轴或图形上的曲线、文字等)都是一个独立的对象。用户可以对其中任何一个图形元素进行单独地修改，而不影响图形的其他部分，具有这样特点的图形称为向量化的绘图。这种向量化的绘图要求给每个图形元素分配一个句柄(handle),以后再对该图形元素做进一步操作时，则只需对该句柄进行操作即可。

MATLAB 5.0版进一步加强了图形绘制的功能，而 5.3版绘图又具有自己的新特色。例如它提供了新的图形编辑程序，并定义了一些新的三维绘图函数等。本章将主要介绍 MATLAB 5.3版本的应用与特性，并介绍部分有关句柄图形学的内容。其余有关句柄图形学的问题，如窗口特性设置、图形界面设计等项内容将在第 6章中讲述图形界面设计内容时详细介绍。MATLAB 6也在图形显示，特别是三维图形显示与照相机参数设置等方面引入了新鲜的内容。

MATLAB定义的各种图形对象及其关系如下图所示。

获取和改变对象的属性可以采用 get()和 set()函数对来实现。

>> set(句柄,属性1,属性值1,属性2,属性值2,...)

>>属性值=get(句柄，属性)

坐标轴对象时 MATLAB图形中常用的对象，坐标轴对象可以用 MATLAB 5.3上的菜单项添加。添加之后，可以用鼠标改变其大小和形状，其他一些属性说明如下：

Box属性:表示是否需要坐标轴上的方框，选项可以为'on'和'off',默认的值为'on'。本书中在后面介绍属性值时，将把默认的属性值列在前面。

ColorOrder属性:设置多条曲线的颜色顺序,应该为一个 n x 3矩阵，可以由 colormap()函数来设置。

GridLineStyle属性:网格线类型，如实线、虚线等，其设置类似于 plot()函数的选项，默认值为':',见前面的表格。

NextPlot属性:表示坐标轴图形的更新方式，'replace'是默认的选项，表示重新绘制，而'add'选项表示在原来的图形上叠印，它相当于直接使用 hold on命令的效果。

Title属性:本坐标轴标题的句柄。而其具体内容由 title()函数设定，由此句柄就可以访问到原来的标题了。

XLabel属性: x轴标注的句柄，其内容由 xlabel()函数设定。此外，类似地还有 YLabel和 ZLabel属性等。

XDir属性: x轴方向,可以选择'normal'(正向)和'rev'(逆向),此外 YDir和 ZDir属性也是类似的。

XGrid属性:表示 x轴是否加网格线，可选值为'off'和'on',此外还类似地有 YGrid和 ZGrid选项。

XLim属性: x轴上下限，以向量 [xm,xM]形式给出。此外，还有 YLim和 ZLim属性，前面介绍的 axis()函数实际上是对这些属性的直接赋值。

XScale属性: x轴刻度类型设置，可以为'linear'(线性的)和'log'(对数的)。此外还有 YScale和 ZScale属性。

XTick和 XTickLabel属性: XTick属性将给出 x轴上标尺点值的向量，而 XTickLabel将存放这些标尺点上的标记字符串。对 y和 z轴也将有相应的标尺属性，如 ZTick等。

MATLAB图形上的文字修饰( 00-12-12)

文字标注是图形修饰中的重要因素，它可以是用户在窗口上随意添加的字符说明，还可以是坐标轴对象中所用到的刻度标志等。字符对象的常用属性如下：

Color属性:字符的颜色。该属性的属性值是一个 1x3颜色向量。

FontAngle属性:字体倾斜形式。如正常'normal'和斜体'italic'等。

FontName属性:字体的名称。如'Times New Roman'与'Courier'等。

FontSize属性:字号大小。默认以 pt为单位，属性值应该为实数。

FontWeight属性:字体是否加黑。可以选择'light'、'normal'(默认值)、'demi'和'bold' 4个选项,其颜色逐渐变黑。

HorizontalAlignment属性:表示文字的水平对齐方式。可以有'left'(按左边对齐)、'center'

(居中对齐)、'right'(按右边对齐)三种选择。类似地，对字符矩阵的位置还有VerticalAlignment属性。

FontUnits属性:字体大小的单位。如'points'(磅数，即 pt)为默认的值，此外，还可以使用如下单位'inches'(英寸)、'centimeters'(厘米)、'normalized'(归一值)与'pixels'(像素)等。

Rotation属性:字体旋转角度。可以为任何数值。

Editing属性:是否允许交互式修改。选项可以为'on'和'off'。

String属性:构成本字符对象的字符串。可以是字符串矩阵。

Interpreter属性:是否允许 TeX格式。选项为'tex'(允许 TeX格式)和'none'(不允许)两种，前者显示的效果好，而后者速度快。

Extent属性:字符串所在的位置范围，是只读型的，1x4向量，前两个值表示字符串所在位置的左下角坐标，而后两个分量分别为字符对象的长和高。

MATLAB字符串中可以直接使用的一些 TeX命令见表 4-3。

>> t=['\partial(f_ip)/\partialt=-\Sigma_{i=1}^n\partial(f_ip)/',...

'\partialx_i+ 0.5\Sigma_{i=1}^n\Sigma_{j=1}^n',...

'\partial^2(b_{ij}p)/\partialx_i\partialx_j'];

tt=str2mat(t,'Y(\omega)=\int_0^\infty y(t)e^{-j\omegat}dt');

[x,y]=ginput(1); text(x,y,tt);

则将得出如下图所示的结果。看见较复杂的数学公式也可以在 MATLAB窗口中显示出来。

〖例〗分形理论是一个很有趣的领域，在这里我们给出一个简单的例子。任意选定一个二维平面上的初始点坐标(x0, y0),假设我们可以生成一个在 [0,1]区间上均匀分布的随机数 gi,那么根据其取值的大小，可以按下面的公式生成一个新的坐标点(x1,y1):

从新坐标再根据随机数计算下一个点，如此类推。可以将上面的算法编写出下面的 MATLAB函数

function [x,y]=frac_tree(x0,y0,v,N)

x=[x0; zeros(N-1,1)]; y=[y0; zeros(N-1,1)];

if vv<0.05, y(i)=0.5*y(i-1);

x(i)=0.42*(x(i-1)-y(i-1)); y(i)=0.2+0.42*(x(i-1)+y(i-1));

x(i)=0.42*(x(i-1)+y(i-1)); y(i)=0.2-0.42*(x(i-1)-y(i-1));

x(i)=0.1*x(i-1); y(i)=0.1*y(i-1)+0.2;

调用此函数，我们可以由下面的 MATLAB命令生成 10,000个这样的点，并将这些点在 MATLAB图形窗口中用点的形式表示出来，如图所示。

>> N=10000; v=rand(N,1);

h=plot(x(1:10000),y(1:10000),'.'),

给出下面的命令可以设置绘图点的大小：

>> set(h,'MarkerSize',4)

对大的 N值，计算量大，可以考虑采用MEX C格式改写 MATLAB函数以加快速度。

MATLAB其他二维图形绘制函数( 00-12-21)

除了标准的 plot()函数外，MATLAB还提供了一些其他函数，具体调用格式和意义请见下表

彗星状轨迹绘制：考虑一个给定函数

选定自变量~$x$的变化范围为 x属于 [-p,p],则可以由下面的函数绘制出不同模式的图形。

y=tan(sin(x))-sin(tan(x)); comet(x,y);

极坐标曲线绘制：用 polar(r,t)函数，其中 r为幅值向量，t为角度向量。

〖例〗绘制 r=cos(5q/4)+1/3;其中 q属于[0,8p],绘制极坐标曲线。

>> t=0:.1:8*pi; r=cos(5*t/4)+1/3;

利用下面的 MATLAB提供的绘图命令可以绘制出各种各样的二维曲线。

>> x=-2:0.1:2; y=sin(x);

feather(x,y); xlabel('(a) feather()')

stairs(x,y); xlabel('(b) stairs()')

stem(x,y); xlabel('(c) stem()')

fill(x,y,'r'); xlabel('(d) fill()')

考察 MATLAB的 Gauss伪随机数发生函数 randn()的分布效果，首先生成 30,000个 Gauss伪随机数，然后由 hist()函数绘制出该伪随机数的分布函数，并和概率密度的理论值

相比较。这一分析的 MATLAB语句如下

>> y=randn(1,30000); xx=-3.8:0.4:3.8;

zz=hist(y,xx); zz=zz/(30000*0.4);

y1=1/sqrt(2*pi)*exp(-x1.^2/2);

hold on, plot(x1,y1); hold off

半对数与全对数坐标系:可以使用 semilogx(), semilogy()和 loglog()。

>> theta=0:0.1:6*pi; r=cos(theta/3)+1/9;

subplot(2,2,1), polar(theta, r);

subplot(2,2,2); plot(theta, r);

subplot(2,2,3); semilogx(theta, r); grid

subplot(2,2,4); semilogy(theta, r), grid

MATLAB语言的三维曲线绘制( 00-12-27)

类似于二维曲线，三维曲线的标准绘制函数为 plot3()。例如，x=cos(t), y=sin(t)和 z=t的数学关系可以由下面语句绘制出来：

set(h,'LineWidth',4*get(h,'LineWidth'))

可以由 mesh()函数绘制，其调用方法是 mesh(x,y,z),其中 x, y, z是网格上的三坐标矩阵。一般情况下，x和 y由 meshgrid()函数生成。

〖例4-17〗考虑下面给出的二元函数，在 x, y平面内选择一个区域，然后绘制出

首先可以调用 meshgrid()函数生成 x和 y平面的网格表示。该函数的调用意义十分明显，即可以产生一个横坐标起始于-3,中止于 3,步距为 0.1;纵坐标起始于-2,中止于2,步距为 0.1的网格分割。然后由公式计算出曲面的 z矩阵。最后调用 mesh()函数绘制曲面的三维表面网格图形。

>> [x,y]= meshgrid(-3:0.1:3,-2:0.1:2);

z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);

同样的数据在 surf()函数下能得出如下所示的表面图(a)。在绘图后再给出 colorbar目录，则将得出如(b)图所示的带有高度指示的三维表面图。

surf()和 mesh()函数绘制出来的三维图实际上是一个 MATLAB图形对象，它有各种各样的属性，例如，其 MeshStyle属性表示其网格的类型，既可以设置成水平的，又可以设置成垂直的。下面的语句将得出下图的网格效果：

>> [x,y]= meshgrid(-3:0.1:3,-2:0.1:2); z=(x.^2-2*x).*exp(-x.^2-y.^2-x.*y);

h=surf(x,y,z), axis([-3 3-2 2-0.7 1.5]); set(h,'MeshStyle','row');

figure; h1=surf(x,y,z), axis([-3 3-2 2-0.7 1.5]); set(h1,'MeshStyle','column');

MATLAB在三维图绘制时，表面着色采用了各种各样的插值方法，其中 shading flat和 shading interp两个命令将方便得出如下的图形。前者将各个表面块用同样的颜色表示，而后者对表面块的着色也进行了插值处理，使其表面显得更光滑。

从 MATLAB 5.3版开始，就提供了图形编辑的方便功能。在标准的MATLAB图形窗口中有一个“图形编辑工具条”，其中提供了各种工具，允许用户自由地在图形上添加文字，箭头、曲线等，还允许用户任意地进行三维图的视角变换。除了工具条上的工具外，还允许用户自如地在图形窗口上添加、调整坐标系或进行一些标注文字的修饰。典型窗口及编辑工具条如下所示。

如果想修改某个曲线的特征，则可以在编辑状态下(即按下工具条中左边的箭头按钮)，首先单击想改动的对象来选择它，然后右击鼠标键，得出相应的快捷菜单，从中选择相应的菜单项，从得出的对话框中对选中对象的属性进行修改。

对三维图形对象，还可以用工具条中最右边的按钮来控制三维图的旋转。

©2000版权所有转载请注明出处并加上本站链接

(本站版面设计参考了CTeX网站的主页，并得到网站版主aloft与eggs的极大帮助，特此致谢)

主页维护:薛定宇自2000年11月3日访问量(“炎黄在线”计数器)