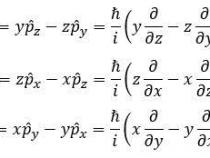直角坐标系中角动量算符及三个分量算符的表达式

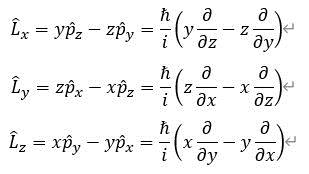
一、直角坐标系中角动量算符及三个分量算符的表达式

1、直角坐标系中角动量算符及三个分量算符的表达式如图：

2、角动量促使在旋转方面的运动得以数量化。在孤立系统里，如同能量和动量，角动量是守恒的。在量子力学里，因为角动量的计算实现于描述量子系统的波函数，而不是经典地实现于一点或一刚体。

3、内积的结果是动量本征波函数不能被归一化。积分在通常的意义下是发散的，这一情况在量子理论中对连续谱的情形具有普遍性：连续谱的本征态不是平方可积的。

4、实际上，在通常意义下连续谱的本征态不能归一化到1，而是归一化成函数。这是因为连续谱的本征函数满足积分。

二、如何求动量算符的本征值和本征函数

1、在一维情况下，动量算符的本征方程可以表示为：

(\hat{P}|\psi_p\rangle=p|\psi_p\rangle)

其中，(\hat{P})是动量算符，(p)是动量的本征值，(|\psi_p\rangle)是对应的本征函数。

2、在坐标表象中，动量算符的本征函数可以表示为平面波的形式：

其中，(C)是归一化常数，(p)是动量的本征值，(x)是位置变量，(\hbar)是约化普朗克常数。

动量算符是在量子力学中表示微观粒子的动量的算符。动量算符是表示力学量的厄米算符。动量算符的本征函数是描述动量算符作用下的量子态的波函数。根据量子力学的理论，动量算符的本征函数可以通过解动量算符的本征方程得到。

动量算符的本征方程可以通过以下步骤求解：

首先，我们需要确定动量算符的表达式。在一维情况下，动量算符可以表示为(\hat{P}=-i\hbar\frac{\partial}{\partialx})，其中(\hbar)是约化普朗克常数。

接下来，我们将动量算符作用在本征函数上，得到本征方程：

(\hat{P}|\psi_p\rangle=p|\psi_p\rangle)

其中，(\hat{P})是动量算符，(p)是动量的本征值，(|\psi_p\rangle)是对应的本征函数。

将动量算符作用在本征函数上，得到：

(-i\hbar\frac{\partial}{\partialx}\psi_p(x)=p\psi_p(x))

对上述方程进行求解，可以得到动量算符的本征函数：

其中，(C)是归一化常数，(p)是动量的本征值，(x)是位置变量。

三、角动量有哪些表达方式

1、直角坐标系中角动量算符及三个分量算符的表达式如图：

2、角动量促使在旋转方面的运动得以数量化。在孤立系统里，如同能量和动量，角动量是守恒的。在量子力学里，因为角动量的计算实现于描述量子系统的波函数，而不是经典地实现于一点或一刚体。

3、内积的结果是动量本征波函数不能被归一化。积分在通常的意义下是发散的，这一情况在量子理论中对连续谱的情形具有普遍性：连续谱的本征态不是平方可积的。

4、实际上，在通常意义下连续谱的本征态不能归一化到1，而是归一化成函数。这是因为连续谱的本征函数满足积分。