如何使用Python实现斐波那契Fibonacci函数

一、如何使用Python实现斐波那契Fibonacci函数

这篇文章主要介绍了如何使用Python实现斐波那契Fibonacci函数相关资料,需要的朋友可以参考下

Fibonacci斐波那契数列，很简单，就是一个递归嘛，学任何编程语言可能都会做一下这个。

最近在玩Python，在粗略的看了一下Learning Python和Core Python之后，偶然发现网上有个帖子Python程序员的进化写的很有意思。于是打算仿照一篇，那篇帖子用了十余种方法完成一个阶乘函数，我在这里会用九种不同的风格写出一个Fibonacci函数。

要求很简单，输入n，输出第n个Fibonacci数，n为正整数

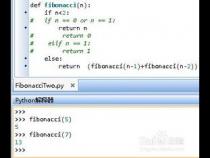
1）第一次写程序的Python程序员：

return nth fibonacci number说明：

第一次写程序的人往往遵循人类语言的语法而不是编程语言的语法，就拿我一个编程很猛的哥们来说，他写的第一个判断闰年的程序，里面直接是这么写的：如果year是闰年，输出year是闰年，否则year不是闰年。

2）刚学Python不久的的C程序员：

在刚接触Python时，用缩进而非大括号的方式来划分程序块这种方式我是很不适应的，而且每个语句后面没有结束符，所以每次写完一个Python函数之后干的第一件事一般就是一边注释大括号，一边添加漏掉的冒号。

return 1 and n<=2 or fib(n-1)+fib(n-2)说明：

看了Learning Python之后，才知道Python没有三元操作符？，不过鉴于Python里bool值比较特殊（有点像C，非零即真，非空即真），再加上Python的逻辑语句也是支持短路求值（Short-Circuit Evaluation）的，这就可以写出一个仿？语句出来。

fib=lambda n:1 if n<=2 else fib(n-1)+fib(n-2)说明：

lambda关键字我曾在C#和Scheme里面用过，Python里面的lambda比C#里简便，并很像Scheme里的用法，所以很快就适应了。在用Python Shell声明一些小函数时经常用这种写法。

5）刚学完数据结构的Python程序员：

前面的Fibonacci函数都是树形递归的实现，哪怕是学一点算法就应该知道这种递归的低效了。在这里从树形递归改为对应的迭代可以把效率提升不少。

Python的元组赋值特性是我很喜欢的一个东东，这玩意可以把代码简化不少。举个例子，以前的tmp=a;a=b;b=tmp;可以直接用一句a,b=b,a实现，既简洁又明了。

6）正在修SICP课程的Python程序员：

else: return fib_iter(n-1,y,x+y)

在这里我使用了Scheme语言中很常见的尾递归（Tail-recursion）写法。Scheme里面没有迭代，但可以用不变量和尾递归来模拟迭代，从而实现相同的效果。不过我还不清楚Python有没有对尾递归做相应的优化，回头查一查。

PS：看过SICP的同学，一眼就能看出，这个程序其实就是SICP第一章里的一个例子。

fib=lambda n,x=0,y=1:x if not n else f(n-1,y,x+y)说明：

基本的逻辑和上面的例子一样，都是尾递归写法。主要的区别就是利用了Python提供的默认参数和三元操作符，从而把代码简化至一行。至于默认参数，学过C++的同学都知道这玩意，至于C#4.0也引入了这东东。

8）刚修完线性代数的Python程序员：

m[0].append(a[0][0]*b[0][0]+a[0][1]*b[1][0])

m[0].append(a[0][0]*b[0][1]+a[0][1]*b[1][1])

m[1].append(a[1][0]*b[0][0]+a[1][1]*b[1][0])

m[1].append(a[1][0]*b[1][0]+a[1][1]*b[1][1])

m.append(a[0][0]*b[0][0]+a[0][1]*b[1][0])

m.append(a[1][0]*b[0][0]+a[1][1]*b[1][0])

return m2(reduce(m1,[[[0,1],[1,1]] for i in range(n)]),[[0],[1]])[0]说明：

这段代码就不像之前的代码那样清晰了，所以先介绍下原理（需要一点线性代数知识）：

首先看一下之前的迭代版本的Fibonacci函数，很容易可以发现存在一个变换：y->x, x+y->y。换一个角度，就是[x,y]->[y,x+y]。

在这里，我声明一个二元向量[x,y]T，它通过一个变换得到[y,x+y]T，可以很容易得到变换矩阵是[[1,0],[1,1]]，也就是说：[[1,0],[1,1]]*[x,y]T=[y,x+y]T

令二元矩阵A=[[1,0],[1,1]]，二元向量x=[0,1]T，容易知道Ax的结果就是下一个Fibonacci数值，即：

A?x=[fib(n),fib(n-1)]T也就是说可以通过对二元向量[0,1]T进行n次A变换，从而得到[fib(n),fib(n+1)]T，从而得到fib(n)。

在这里我定义了一个二元矩阵的相乘函数m1，以及一个在二元向量上的变换m2，然后利用reduce操作完成一个连乘操作得到A?x，最后得到fib(n)。

9）准备参加ACM比赛的Python程序员：

#initialize an empty matrix filled with zero

result=[[0 for i in range(len(rhm[0]))] for j in range(len(rhm))]

result[i][j]+=lhm[i][k]*rhm[k][j]

return matrix_mul(mat,fib_iter(mat,n-1))

return matrix_square(fib_iter(mat,n/2))

return matrix_mul(fib_iter(lhm,n),rhm)[0][0]说明：

看过上一个fib函数就比较容易理解这一个版本了，这个版本同样采用了二元变换的方式求fib(n)。不过区别在于这个版本的复杂度是lgn，而上一个版本则是线性的。

这个版本的不同之处在于，它定义了一个矩阵的快速求幂操作fib_iter，原理很简单，可以类比自然数的快速求幂方法，所以这里就不多说了。

PS：虽然说是ACM版本，不过说实话我从来没参加过那玩意，毕竟自己算法太水了，那玩意又太高端??只能在这里YY一下鸟~

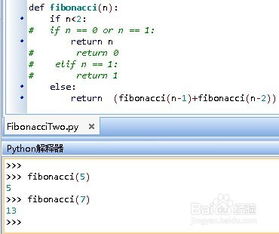
python中，最基本的那种递归（如下fib1)效率太低了，只要n数字大了运算时间就会很长；而通过将计算的指保存到一个dict中，后面计算时直接拿来使用，这种方式成为备忘(memo)，如下面的fib2函数所示，则会发现效率大大提高。

在n=10以内时，fib1和fab2运行时间都很短看不出差异，但当n=40时，就太明显了，fib1运行花了35秒，fab2运行只花费了0.00001秒。

jay@jay-linux:~/workspace/python.git/py2014$ python fibonacci.py

2014-10-16 16:29:10.480035这两个计算Fibonacci数列的函数，如下：

return fib1(n- 1)+ fib1(n- 2)

if __name__=='__main__':

print(datetime.datetime.now())

print('fib1(%d)=%d'%(n, fib1(n)))

print(datetime.datetime.now())

print('fib2(%d)=%d'%(n, fib2(n)))

print(datetime.datetime.now())后记：

由于刚学习Python没多久，所以对其各种特性的掌握还不够熟练。与其说是我在用Python写程序，倒不如说我是在用C，C++，C#或是Scheme来写程序。至于传说中的Pythonic way，我现在还没有什么体会，毕竟还没用Python写过什么真正的程序。

Learning Python和Core Python都是不错的Python入门书籍，前者更适合没有编程基础的人阅读。

Python是最好的初学编程入门语言，没有之一。所以它可以取代Scheme成为MIT的计算机编程入门语言。

二、python做斐波那契数列。

1、直接创建一个类然后调用下面的def函数即可

2、def get_Fibonacci_sequence(n):

3、'''输入n,遍历到第n位的斐波那契数列'''

4、if n>=3:#即等于>2相当于1,2位特殊处理

5、for i in range(n-1):#操作次数是n-1，去除一次第一位的操作

6、print(b)#这里选择先改变再输出，可以减少1次的循环

7、'''输入n,遍历到第n位的斐波那契数列的第n位数'''

8、if n>= 3:#即等于>2相当于1,2位特殊处理

9、for i in range(n- 1):#操作次数是n-1，去除一次第一位的操作

10、#这里选择先改变再输出，可以减少1次的循环

11、def get_Fibonacci_Num_recursion(n):

12、'''输入n,遍历到第n位的斐波那契数列的第n位数,递归实现'''

13、if n==1 or n==2:#特别注意，这里要用逻辑或判断，不能直接用或判断，

14、return get_Fibonacci_Num_recursion(n-1)+get_Fibonacci_Num_recursion(n-2)

15、print(get_Fibonacci_Num_recursion(11))

三、Python实现斐波那契数列的方法以及优化

1、斐波那契数列（意大利语：Successione di Fibonacci）的定义：

2、斐波那契数列由0和1开始，之后的每个斐波那契数就是由之前的两数相加而得出。具体数值如下：

3、 0，1， 1， 2， 3， 5， 8， 13， 21， 34， 55， 89， 144， 233， 377， 610,..............

4、特别注意：F(0)代表的是第一个数值，数列下标由0开始。

5、代码如上，用了迭代的算法计算每个数值，每个N值最大运行N-1次循环，算法比递归要高效很多。递归代码如下：