java面试题 很急 谢谢

一、java面试题 很急 谢谢

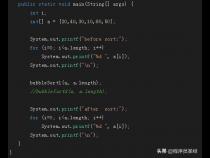
2,归并排序(merge sort)体现了分治的思想，即将一个待排序数组分为两部分，对这两个部分进行归并排序，排序后，再对两个已经排序好的数组进行合并。这种思想可以用递归方式很容易实现。归并排序的时间复杂度为O(nlogn)，空间复杂度为O(n)。

void merge(int data[], int p, int q, int r)

for(i= 0, k= p; i< n1; i++, k++)

for(i= 0, k= q+ 1; i< n2; i++, k++)

for(k= p, i= 0, j= 0; i< n1&& j< n2; k++)

for(j= i; j< n1; j++, k++)

for(i= j; i< n2; i++, k++)

void merge_sort(int data[], int p, int r)

int data[]={44, 12, 145,-123,-1, 0, 121};

printf("-------------------------------merge sort----------------------------\n");

4.对于有n个结点的线性表（e0，e1，…，en-1），将结点中某些数据项的值按递增或递减的次序，重新排列线性表结点的过程，称为排序。排序时参照的数据项称为排序码，通常选择结点的键值作为排序码。

若线性表中排序码相等的结点经某种排序方法进行排序后，仍能保持它们在排序之前的相对次序，称这种排序方法是稳定的；否则，称这种排序方法是不稳定的。

在排序过程中，线性表的全部结点都在内存，并在内存中调整它们在线性表中的存储顺序，称为内排序。在排序过程中，线性表只有部分结点被调入内存，并借助内存调整结点在外存中的存放顺序的排序方法成为外排序。

下面通过一个表格简单介绍几种常见的内排序方法，以及比较一下它们之间的性能特点。

反复从还未排好序的那部分线性表中选出键值最小的结点，并按从线性表中选出的顺序排列结点，重新组成线性表。直至未排序的那部分为空，则重新形成的线性表是一个有序的线性表。

假设线性表的前面I个结点序列e0，e1，…，en-1是已排序的。对结点在这有序结点ei序列中找插入位置，并将ei插入，而使i+1个结点序列e0，e1，…，ei也变成排序的。依次对i=1，2，…，n-1分别执行这样的插入步骤，最终实现线性表的排序。

对当前还未排好序的范围内的全部结点，自上而下对相邻的两个结点依次进行比较和调整，让键值大的结点往下沉，键值小的结点往上冒。即，每当两相邻比较后发现它们的排列顺序与排序要求相反时，就将它们互换。

对直接插入排序一种改进，又称“缩小增量排序”。先将整个待排序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

对冒泡排序的一种本质的改进。通过一趟扫视后，使待排序序列的长度能大幅度的减少。在一趟扫视后，使某个结点移到中间的正确位置，并使在它左边序列的结点的键值都比它的小，而它右边序列的结点的键值都不比它的小。称这样一次扫视为“划分”。每次划分使一个长序列变成两个新的较小子序列，对这两个小的子序列分别作同样的划分，直至新的子序列的长度为1使才不再划分。当所有子序列长度都为1时，序列已是排好序的了。

一种树形选择排序，是对直接选择排序的有效改进。一个堆是这样一棵顺序存储的二叉树，它的所有父结点（e[i]）的键值均不小于它的左子结点（e[2*i+1]）和右子结点（e[2*i+2]）的键值。初始时，若把待排序序列的n个结点看作是一棵顺序存储的二叉树，调整它们的存储顺序，使之成为一个堆，这时堆的根结点键值是最大者。然后将根结点与堆的最后一个结点交换，并对少了一个结点后的n-1结点重新作调整，使之再次成为堆。这样，在根结点得到结点序列键值次最大值。依次类推，直到只有两个结点的堆，并对它们作交换，最后得到有序的n个结点序列。

将两个或两个以上的有序子表合并成一个新的有序表。对于两个有序子表合并一个有序表的两路合并排序来说，初始时，把含n个结点的待排序序列看作有n个长度都为1的有序子表所组成，将它们依次两两合并得到长度为2的若干有序子表，再对它们作两两合并……直到得到长度为n的有序表，排序即告完成。

后面根据各种排序算法，给出了C语言的实现，大家在复习的时候可以做下参考。

for(t=e[i], j=i-1; j>=0&&t<e[j]; j--)

t=e[j]; e[j]=e[j+1]; e[j+1]=t;

for(k=j-h; k>0&&y<e[k]; k-=h)

void r_quick(int e[], int low, int high)

while(i<j&&e[j]>t) j--;

while(i<j&&e[i]<=t) i++;

另外，外排序是对大型文件的排序，待排序的记录存储在外存中，在排序过程中，内存只存储文件的一部分记录，整个排序过程需进行多次的内外存间的交换。

查找就是在按某种数据结构形式存储的数据集合中，找出满足指定条件的结点。

按查找的条件分类，有按结点的关键码查找、关键码以外的其他数据项查找或其他数据项的组合查找等。按查找数据在内存或外存，分内存查找和外存查找。按查找目的，查找如果只是为了确定指定条件的结点存在与否，成为静态查找；查找是为确定结点的插入位置或为了删除找到的结点，称为动态查找。

这里简单介绍几种常见的查找方法。

这是最常见的查找方式。结点集合按线性表组织，采用顺序存储方式，结点只含关键码，并且是整数。如果线性表无序，则采用顺序查找，即从线性表的一端开始逐一查找。而如果线性表有序，则可以使用顺序查找、二分法查找或插值查找。

分块查找的过程分两步，先用二分法在索引表中查索引项，确定要查的结点在哪一块。然后，再在相应块内顺序查找。

对于链接存储线性表的查找只能从链表的首结点开始顺序查找。同样对于无序的链表和有序的链表查找方法不同。

散列表又称杂凑表，是一种非常实用的查找技术。它的原理是在结点的存储位置和它的关键码间建立一个确定的关系，从而让查找码直接利用这个关系确定结点的位置。其技术的关键在于解决两个问题。

二、pascal基础知识

从上面的求解问题过程可以看出，关键在于前三步的解决：第一步就是解决模型的数据结构，第二步是解决问题的算法，第三步是形式化地描写算法。

算法是一组有穷的规则，它们规定了解决某一特定类型问题的一系列运算。算法可以理解为：程序（数据处理）+数据结构（数据组织）。

③输入输出(可以没有输入，但一定有输出)

常见的算法有：穷举法、迭代法、递推法、递归法、回溯法、深度及广度搜索法、动态规划、构造法等等。

1973年，美国学者I.Nassi和B.Shneiderman提出了一种用图形表示算法的方法，称为N-S流程图。N-S图包括顺序、选择和循环三种基本结构。

计算机中的语言分为低级语言和高级语言，而低级语言又分为机器语言和汇编语言。

机器语言是一种CPU的指令系统，它是CPU可以识别的一系列有0和1这种二进制代码组成的指令。它依赖于机器，不同类型的计算机有不同的机器语言，机器语言的程序有许多机器指令组成，每条指令由操作码和地址码组成，数据和指令都放在不同的地址单元中。

汇编语言它是一种符号语言，为了克服机器语言固有的缺陷，20世纪50年代中期出现，将难以记忆和辨别的机器语言操作码用有意义的英文单词作为“助记符”来代替0、1进行编程。

高级语言，不再面向机器，而是接近人类的自然语言。常见的还有C/C++，Pascal,Basic,Java等。

数据类型、常量、变量及说明方法

数据类型确定了该类型数据项的表示、取值范围以及所能参与的运算。在pascal语言中，无论常量还是变量都必须属于一个确定的数据类型。

Pascal提供了丰富的数据类型，可以分为三大类：

①简单类型：分为标准类型（整型、实型、字符型和布尔型）和自定义类型（枚举型和子界型）

②构造类型：分为数组类型、集合类型、记录类型和文件类型

这些数据类型中除了指针类型是动态数据类型外，其他的都是静态数据类型。另外，我们把整型、字符型、布尔型、枚举型和子界型称为顺序类型。

– representative?Getfather(x)

*初始的时候，所有元素各自成为一个集合

* return Getfather(x)=Getfather(y)

–将其中一集合的代表元指向另一集合代表元

– father[x]?Getfather(father[x])

–树上的每棵子树，儿子的值不小于根

–可以将一串连续的数变为一个值