数学里共有哪些类型的函数

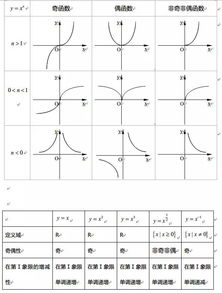
一、数学里共有哪些类型的函数

1、函数的分类方法很多。看你以什么标准分类。比如：

2、以运算的有限和无限,可以分为初等函数，非初等函数。

3、以函数的单调性分类，可以分为定义域上的增函数、减函数，其他函数。

4、以函数的奇偶性分类，可以分为奇函数、偶函数，既是奇函数又是偶函数，非奇非偶函数。

5、以函数的有界性分类，可以分为有界函数，无界函数。

6、以函数的连续性分类，可以分为连续函数，非连续函数（包括离散函数）。

7、以上是基于中学函数的概念（一元单值实函数）的分类。

二、高中数学八大函数是什么啊

1、高中数学八大函数是：幂函数，指数函数，对数函数，反函数，一次函数，二次函数，反比例函数，对勾函数。

2、函数（function），数学术语。其定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。函数的近代定义是给定一个数集A。

3、假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示，函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

4、函数，最早由中国清朝数学家李善兰翻译，出于其著作《代数学》。之所以这么翻译，他给出的原因是“凡此变数中函彼变数者，则此为彼之函数”，也即函数指一个量随着另一个量的变化而变化，或者说一个量中包含另一个量。

5、首先要理解，函数是发生在集合之间的一种对应关系。然后，要理解发生在A、B之间的函数关系有且不止一个。最后，要重点理解函数的三要素。函数的对应法则通常用解析式表示，但大量的函数关系是无法用解析式表示的，可以用图像、表格及其他形式表示。

6、中国古代“函”字与“含”字通用，都有着“包含”的意思。李善兰给出的定义是：“凡式中含天，为天之函数。”中国古代用天、地、人、物4个字来表示4个不同的未知数或变量。凡是公式中含有变量x，则该式子叫做x的函数。

7、“函数”是指公式里含有变量的意思。我们所说的方程的确切定义是指含有未知数的等式。但是方程一词在我国早期的数学专著《九章算术》中，意思指的是包含多个未知量的联立一次方程，即所说的线性方程组。

三、几种常见的函数

常见的函数类型有线性函数、幂函数、三角函数。

1、线性函数：线性函数是最简单的函数类型之一，它表示变量之间的线性关系。线性函数的公式为y=mx+b，其中m是斜率，b是截距。线性函数在图形上表现为一条直线。在实际应用中，线性函数常用于描述两个变量之间的比例关系，例如速度与时间的关系。

2、幂函数：幂函数表示一个变量是另一个变量的指数。幂函数的公式为y=x^n，其中n是指数。幂函数在图形上表现为一条曲线，其形状取决于指数n的值。在实际应用中，幂函数常用于描述变量之间的增长或衰减关系，例如人口增长或病毒传播的模型。

3、三角函数：三角函数是周期性的函数，其表达式为y=sin（x），y=cos（x），y=tan（x）。三角函数在图形上表现为正弦波、余弦波和正切波。在实际应用中，三角函数常用于描述周期性的变化，例如振动、波动和交流电等。

1、数学和科学计算：函数是数学中描述变量之间关系的基本工具。在数学中，函数被广泛应用于代数、几何、微积分等领域。例如，线性函数可以用于解决代数方程和线性规划问题；幂函数可以用于描述指数增长和衰减；而三角函数则常用于解决周期性波动和振动等问题。

2、实际问题建模：函数可以用来描述实际问题中变量之间的关系。通过建立适当的函数模型，可以简化问题并找到解决方案。例如，在经济学中，函数可以用于描述需求、供给、价格之间的关系；在物理学中，函数可以用于描述速度、加速度、时间之间的关系；在生物学中，函数可以用于描述生长、繁殖、死亡等过程。

3、计算机科学：函数在计算机科学中也有广泛的应用。在编程语言中，函数是基本的编程单元，用于实现特定的功能和操作。通过定义函数，可以将复杂的代码块封装起来，提高代码的可读性和可维护性。函数还可以用于实现模块化编程和面向对象编程等设计模式。