软件编程都需要学习哪些知识点呢

一、软件编程都需要学习哪些知识点呢

你好，软件编程专业需要学习的知识点有下面几点：

1.类型不同，结果就是 false。否则，继续比较值。字符串按一般的方式比较。数字遵循二元操作的规则：如果两个操作数都是整数，它们按整数比较；否则，它们先转换为浮点数，然后再做比较。

2.表，用户数据，以及线程都按引用比较：只有两者引用同一个对象时才认为它们相等。每次你创建一个新对象（一张表，一个用户数据，或一个线程），新对象都一定和已有且存在的对象不同。相同引用的闭包一定相等。有任何可察觉的差异（不同的行为，不同的定义）一定不等。

3.你可以通过使用"eq"元方法来改变 Lua比较表和用户数据时的方式。

等于操作不会将字符串转换为数字，反之亦然。即，"0"==0结果为 false，且 t[0]与 t["0"]指代着表中的不同项。

3.~=操作完全等价于(==)操作的反值。

大小比较操作以以下方式进行。如果参数都是数字，它们按二元操作的常规进行。否则，如果两个参数都是字符串，它们的值按当前的区域设置来比较。再则，Lua就试着调用"lt"或是"le"元方法。 a> b的比较被转译为 b< a， a>= b被转译为 b<= a。

中的逻辑操作符有 and， or，以及 not。和控制结构一样，所有的逻辑操作符把 false和 nil都作为假，而其它的一切都当作真。

4.取反操作 not总是返回 false或 true中的一个。与操作符 and在第一个参数为 false或 nil时返回这第一个参数；否则，and返回第二个参数。或操作符 or在第一个参数不为 nil也不为 false时，返回这第一个参数，否则返回第二个参数。 and和 or都遵循短路规则；也就是说，第二个操作数只在需要的时候去求值。

5.你可以通过使用"eq"元方法来改变 Lua比较表和用户数据时的方式。

等于操作不会将字符串转换为数字，反之亦然。即，"0"==0结果为 false，且 t[0]与 t["0"]指代着表中的不同项。

6.~=操作完全等价于(==)操作的反值。

大小比较操作以以下方式进行。如果参数都是数字，它们按二元操作的常规进行。否则，如果两个参数都是字符串，它们的值按当前的区域设置来比较。再则，Lua就试着调用"lt"或是"le"元方法。 a> b的比较被转译为 b< a， a>= b被转译为 b<= a。

7.中的逻辑操作符有 and， or，以及 not。和控制结构一样，所有的逻辑操作符把 false和 nil都作为假，而其它的一切都当作真。

二、与编程有关的数学知识点是那些

1、与编程有关的数学知识点是那些？

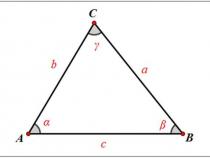
三角函数，立体几何，高等数学。

2、三角函数，立体几何，高等数学。

3、看你要搞哪方面编程了，比如三维变换，那就得搞立体几何

4、除此之外还有统计学，离散数学等……

5、是广西的老人么?好象是..不是很清楚..反正他写的幻方破了吉尼斯记录..就是为北京奥运加油的..

6、加一：一上一，一下五去四，一去九进一

7、加二：二上二，二下五去三，二去八进一

8、加三：三上三，三下五去二，三去七进一

9、加四：四上四，四下五去一，四去六进一

10、加六：六上六，六去四进一，六上一去五进一

11、加七：七上七，七去三进一，七上二去五进一

12、加八：八上八，八去二进一，八上三去五进一

13、加九：九上九，九去一进一，九上四去五进一

14、这个不少呢吧。像家居装饰，喜欢用黄金分割比，让人看着舒服。像存款取款，会用到比率方程等。。。

15、数据结构，线性代数，离散数学，高等数学，要是想深入这也些都是必不可少的

16、要什么级别的？幼儿园？还是大学？

17、关键看你是要编什么，如果是游戏，有可能要用到物理，若是牵涉到一些图像处理，那矩阵理论肯定要知道。网络编程我觉得更需要的是算法的掌握，比如图论。总的来讲，若是有空了解下数学建模会对你很有帮助。

18、知道怎么统计所需要的数字的公式就行~!

19、其实大多数的软件使用者他们的统计方法或学问也不是很高!!

20、 5过一点有且只有一条直线和已知直线垂直

21、 6直线外一点与直线上各点连接的所有线段中，垂线段最短

22、 7平行公理经过直线外一点，有且只有一条直线与这条直线平行

23、 8如果两条直线都和第三条直线平行，这两条直线也互相平行

24、 15定理三角形两边的和大于第三边

25、 16推论三角形两边的差小于第三边

26、 17三角形内角和定理三角形三个内角的和等于180°

27、 18推论1直角三角形的两个锐角互余

28、 19推论2三角形的一个外角等于和它不相邻的两个内角的和

29、 20推论3三角形的一个外角大于任何一个和它不相邻的内角

30、 21全等三角形的对应边、对应角相等

31、 22边角边公理(SAS)有两边和它们的夹角对应相等的两个三角形全等

32、 23角边角公理( ASA)有两角和它们的夹边对应相等的两个三角形全等

33、 24推论(AAS)有两角和其中一角的对边对应相等的两个三角形全等

34、 25边边边公理(SSS)有三边对应相等的两个三角形全等

35、 26斜边、直角边公理(HL)有斜边和一条直角边对应相等的两个直角三角形全等

36、 27定理1在角的平分线上的点到这个角的两边的距离相等

37、 28定理2到一个角的两边的距离相同的点，在这个角的平分线上

38、 29角的平分线是到角的两边距离相等的所有点的集合

39、 30等腰三角形的性质定理等腰三角形的两个底角相等(即等边对等角）

40、 31推论1等腰三角形顶角的平分线平分底边并且垂直于底边

41、 32等腰三角形的顶角平分线、底边上的中线和底边上的高互相重合

42、 33推论3等边三角形的各角都相等，并且每一个角都等于60°

43、 34等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等（等角对等边）

44、 35推论1三个角都相等的三角形是等边三角形

45、 36推论 2有一个角等于60°的等腰三角形是等边三角形

46、 37在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半

47、 38直角三角形斜边上的中线等于斜边上的一半

48、 39定理线段垂直平分线上的点和这条线段两个端点的距离相等

49、 40逆定理和一条线段两个端点距离相等的点，在这条线段的垂直平分线上

50、 41线段的垂直平分线可看作和线段两端点距离相等的所有点的集合

51、 42定理1关于某条直线对称的两个图形是全等形

52、 43定理 2如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线

53、 44定理3两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上

54、 45逆定理如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称

55、 46勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方，即a^2+b^2=c^2

56、 47勾股定理的逆定理如果三角形的三边长a、b、c有关系a^2+b^2=c^2，那么这个三角形是直角三角形

57、 48定理四边形的内角和等于360°

58、 50多边形内角和定理 n边形的内角的和等于（n-2）×180°

59、 51推论任意多边的外角和等于360°

60、 52平行四边形性质定理1平行四边形的对角相等

61、 53平行四边形性质定理2平行四边形的对边相等

62、 54推论夹在两条平行线间的平行线段相等

63、 55平行四边形性质定理3平行四边形的对角线互相平分

64、 56平行四边形判定定理1两组对角分别相等的四边形是平行四边形

65、 57平行四边形判定定理2两组对边分别相等的四边形是平行四边形

66、 58平行四边形判定定理3对角线互相平分的四边形是平行四边形

67、 59平行四边形判定定理4一组对边平行相等的四边形是平行四边形

68、 60矩形性质定理1矩形的四个角都是直角

69、 61矩形性质定理2矩形的对角线相等

70、 62矩形判定定理1有三个角是直角的四边形是矩形

71、 63矩形判定定理2对角线相等的平行四边形是矩形

72、 64菱形性质定理1菱形的四条边都相等

73、 65菱形性质定理2菱形的对角线互相垂直，并且每一条对角线平分一组对角

74、 66菱形面积=对角线乘积的一半，即S=（a×b）÷2

75、 67菱形判定定理1四边都相等的四边形是菱形

76、 68菱形判定定理2对角线互相垂直的平行四边形是菱形

77、 69正方形性质定理1正方形的四个角都是直角，四条边都相等

78、 70正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角

79、 71定理1关于中心对称的两个图形是全等的

80、 72定理2关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分

81、 73逆定理如果两个图形的对应点连线都经过某一点，并且被这一

82、点平分，那么这两个图形关于这一点对称

83、 74等腰梯形性质定理等腰梯形在同一底上的两个角相等

84、 76等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形

85、 78平行线等分线段定理如果一组平行线在一条直线上截得的线段

86、相等，那么在其他直线上截得的线段也相等

87、 79推论1经过梯形一腰的中点与底平行的直线，必平分另一腰

88、 80推论2经过三角形一边的中点与另一边平行的直线，必平分第

89、 81三角形中位线定理三角形的中位线平行于第三边，并且等于它

90、 82梯形中位线定理梯形的中位线平行于两底，并且等于两底和的

91、 83(1)比例的基本性质如果a:b=c:d,那么ad=bc

92、 84(2)合比性质如果a／b=c／d,那么(a±b)／b=(c±d)／d

93、 85(3)等比性质如果a／b=c／d=…=m／n(b+d+…+n≠0),那么

94、 86平行线分线段成比例定理三条平行线截两条直线，所得的对应

95、 87推论平行于三角形一边的直线截其他两边（或两边的延长线），所得的对应线段成比例

96、 88定理如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边

97、 89平行于三角形的一边，并且和其他两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例

98、 90定理平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似

99、 91相似三角形判定定理1两角对应相等，两三角形相似（ASA）

100、 92直角三角形被斜边上的高分成的两个直角三角形和原三角形相似

101、 93判定定理2两边对应成比例且夹角相等，两三角形相似（SAS）

102、 94判定定理3三边对应成比例，两三角形相似（SSS）

103、 95定理如果一个直角三角形的斜边和一条直角边与另一个直角三

104、角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似

105、 96性质定理1相似三角形对应高的比，对应中线的比与对应角平

106、 97性质定理2相似三角形周长的比等于相似比

107、 98性质定理3相似三角形面积的比等于相似比的平方

108、 99任意锐角的正弦值等于它的余角的余弦值，任意锐角的余弦值等

109、 100任意锐角的正切值等于它的余角的余切值，任意锐角的余切值等

110、 101圆是定点的距离等于定长的点的集合

111、 102圆的内部可以看作是圆心的距离小于半径的点的集合

112、 103圆的外部可以看作是圆心的距离大于半径的点的集合

113、 105到定点的距离等于定长的点的轨迹，是以定点为圆心，定长为半

114、 106和已知线段两个端点的距离相等的点的轨迹，是着条线段的垂直

115、 107到已知角的两边距离相等的点的轨迹，是这个角的平分线

116、 108到两条平行线距离相等的点的轨迹，是和这两条平行线平行且距

117、 109定理不在同一直线上的三点确定一个圆。

118、 110垂径定理垂直于弦的直径平分这条弦并且平分弦所对的两条弧

119、 111推论1①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧

120、②弦的垂直平分线经过圆心，并且平分弦所对的两条弧

121、③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧

122、 112推论2圆的两条平行弦所夹的弧相等

123、 113圆是以圆心为对称中心的中心对称图形

124、 114定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦

125、 115推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两

126、弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等

127、 116定理一条弧所对的圆周角等于它所对的圆心角的一半

128、 117推论1同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等

129、 118推论2半圆（或直径）所对的圆周角是直角；90°的圆周角所

130、 119推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形

131、 120定理圆的内接四边形的对角互补，并且任何一个外角都等于它

132、 122切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线

133、 123切线的性质定理圆的切线垂直于经过切点的半径

134、 124推论1经过圆心且垂直于切线的直线必经过切点

135、 125推论2经过切点且垂直于切线的直线必经过圆心

136、 126切线长定理从圆外一点引圆的两条切线，它们的切线长相等，

137、圆心和这一点的连线平分两条切线的夹角

138、 127圆的外切四边形的两组对边的和相等

139、 128弦切角定理弦切角等于它所夹的弧对的圆周角

140、 129推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等

141、 130相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积

142、 131推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的

143、 132切割线定理从圆外一点引圆的切线和割线，切线长是这点到割

144、线与圆交点的两条线段长的比例中项

145、 133推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等

146、 134如果两个圆相切，那么切点一定在连心线上

147、 135①两圆外离 d＞R+r②两圆外切 d=R+r

148、④两圆内切 d=R-r(R＞r)⑤两圆内含d＜R-r(R＞r)

149、 136定理相交两圆的连心线垂直平分两圆的公共弦

150、⑴依次连结各分点所得的多边形是这个圆的内接正n边形

151、⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形

152、 138定理任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆

153、 139正n边形的每个内角都等于（n-2）×180°／n

154、 140定理正n边形的半径和边心距把正n边形分成2n个全等的直角三角形

155、 141正n边形的面积Sn=pnrn／2 p表示正n边形的周长

156、 142正三角形面积√3a／4 a表示边长

157、 143如果在一个顶点周围有k个正n边形的角，由于这些角的和应为

158、 360°，因此k×(n-2)180°／n=360°化为（n-2）(k-2)=4

159、 145扇形面积公式：S扇形=n兀R^2／360=LR／2

160、 146内公切线长= d-(R-r)外公切线长= d-(R+r)

161、乘法与因式分 a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b(a2+ab+b2)

162、三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b

163、一元二次方程的解-b+√(b2-4ac)/2a-b-√(b2-4ac)/2a

164、根与系数的关系 X1+X2=-b/a X1*X2=c/a注：韦达定理

165、 b2-4ac=0注：方程有两个相等的实根

166、 b2-4ac>0注：方程有两个不等的实根

167、 b2-4ac<0注：方程没有实根，有共轭复数根

168、 sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA

169、 cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB

170、 tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB)

171、 ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)

172、 tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga

173、 cos2a=cos2a-sin2a=2cos2a-1=1-2sin2a

174、 sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)

175、 cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)

176、 tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))

177、 ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))

178、 2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)

179、 2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)

180、 sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2)

181、 tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB

182、 ctgA+ctgBsin(A+B)/sinAsinB-ctgA+ctgBsin(A+B)/sinAsinB

183、 1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n2

184、 2+4+6+8+10+12+14+…+(2n)=n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6

185、 13+23+33+43+53+63+…n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3

186、正弦定理 a/sinA=b/sinB=c/sinC=2R注：其中 R表示三角形的外接圆半径

187、余弦定理 b2=a2+c2-2aosB注：角B是边a和边c的夹角

188、圆的标准方程(x-a)2+(y-b)2=r2注：（a,b）是圆心坐标

189、圆的一般方程 x2+y2+Dx+Ey+F=0注：D2+E2-4F>0

190、抛物线标准方程 y2=2px y2=-2px x2=2py x2=-2py

191、直棱柱侧面积 S=c*h斜棱柱侧面积 S=c'*h

192、正棱锥侧面积 S=1/2c*h'正棱台侧面积 S=1/2(c+c')h'

193、圆台侧面积 S=1/2(c+c')l=pi(R+r)l球的表面积 S=4pi*r2

194、圆柱侧面积 S=c*h=2pi*h圆锥侧面积 S=1/2*c*l=pi*r*l

195、弧长公式 l=a*r a是圆心角的弧度数r>0扇形面积公式 s=1/2*l*r

196、锥体体积公式 V=1/3*S*H圆锥体体积公式 V=1/3*pi*r2h

197、(对不起，太多点题目好难找，不过这个网址:czsx../就有初中数学题目大全）

三、学编程应该先学什么

1、可以先学 Pascal。 Pascal是一门很好的教学语言。然后对过程式编程有些了解以后可以学习数据结构，C和 C++。然后可以学一下 Java或 C#。当然我的建议只是帮助你能够了解过程式和面向对象的编程。至于要进入IT业，方向和门类很多，所以学什么更好不能一概而论。

2、如果希望能够进入计算机系，拿一个“科班出身”的学位，从Pascal学起不错，可以把Structured programming的基础打好。但是大部分人，从Visusal Basic学起更能够速成，并增加自信。

3、大计算机科学的底子：c，c++，离散数学，数据结构，数据库，软件工程，（可参考MIT Open Courseware)。业余者自修：Visual Basic， Scripting，Frontpage， Flash。

4、C++是C的延伸，所以两者有很大的重叠部分，分不清很正常。我觉得C是基础。用C能够熟练地写程序以后，再逐渐接触C++的程序设计理念可能更好一些。

5、“学习一门语言的最好方法是用它来编程序”。

6、最后，不能只学语言。许多大学生认为学最新的计算机语言、技术、标准是最好的铺路方法，因为许多公司招聘时要求这些方面的经验。这些新技术虽然该学，但是学习计算机基础课程更重要，因为计算机语言和开发平台日新月异，但是万变不离其宗的就是那些基础课程：数据结构、算法、编译原理、计算机组成、关系型数据库原理等。有位同学生动地在“开复学生网”上把这些基础课程比拟为内功，把新的语言、技术、标准比拟为外功。只追寻时髦的学生最后只懂招式，没有功力，是不可能成为高手的。