什么是对勾函数,双刀函数

一、什么是对勾函数,双刀函数

1、对勾函数是一种类似于反比例函数的一般双曲函数，是形如f(x)=ax+b/x（a>0）的函数。

2、对勾函数是一种类似于反比例函数的一般函数，又被称为“双勾函数”、“勾函数”、"对号函数"、“双飞燕函数”等。也被形象称为“耐克函数”或“耐克曲线”。

3、所谓的对勾函数（双曲函数），是形如f(x)=ax+b/x（a>0)的函数。由图像得名。

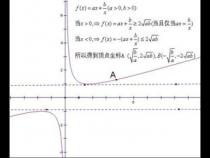
4、对勾函数是数学中一种常见而又特殊的函数，见图示，在作图时最好画出渐近线y=ax。

5、当x>0时，f(x)=ax+b/x有最小值（这里为了研究方便，规定a>0，b>0），也就是当x=sqrt(b/a）时（sqrt表示求二次方根）是奇函数。

6、减区间：{x|-k≤x<0}和{x|0<x≤k}

7、变化趋势：在y轴左边，增减，在y轴右边，减增，是两个勾。

8、过反比例函数上任意一点分别作两坐标轴的平行线，与两坐标轴围成的平行四边形面积等于|b|。

9、对勾函数的图像是分别以y轴和y=ax为渐近线的两支双曲线，且图像上任意一对勾函数点到两条渐近线的距离之积恰为渐近线夹角(0-180°)的正弦值与|b|的乘积。

10、对勾函数性质的研究离不开均值不等式。说到均值不等式，其实也是根据二次函数得来的。我们都知道（a-b）^2≥0

11、展开，得a^2-2ab+b^2≥0，即a^2+b^2≥2ab.

12、两边同时加上2ab，整理得(a+b)^2≥4ab，

13、两边开平方，就得到了均值定理的公式：a+b≥2√ab

14、将ax+b/x中ax看做a，b/x看做b代入上式，得

15、这里有个规定：当且仅当ax=b/x时取到最小值，解出x=sqrt(b/a），对应的f(x)=2sqrt(ab）。

16、我们再来看看均值不等式，它也可以写成这样：（a+b)/2≥sqrt(ab），前式大家都知道，是求平均数的公式。那么后面的式子呢？也是平均数的公式，但不同的是，前面的称为算术平均数，而后面的则称为几何平均数，总结一下就是算术平均数绝对不会小于几何平均数。这些知识点也是非常重要的。

17、其实用导数也可以研究对勾函数的性质。不过首先要会负指数幂的换算，这也很简单，但要熟练掌握。举几个例子：1/x=x^-1，4/x^2=4x^-2。明白了吧，x为分母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx^-1，求导方法一样，求得的导函数为a+(-b)x^-2，令f'(x)=0，计算得到b=ax2，结果仍然是x=sqrt(b/a），如果需要的话算出f(x）就行了。平时做题的时候用导数还是均值定理，就看你喜欢用哪个了。不过注意均值定理最后的讨论，有时ax≠b/x，就不能用均值定理了。

18、上述研究都是建立在x>0的基础上的，不过对勾函数是奇函数，所以研究出正半轴图像的性质后，自然能补出对称的图像。如果出现平移了的问题（图像不再规则），就先用平移公式或我总结出的平移规律还原以后再研究，这个能力非常重要，一定要多练，争取做到特别熟练的地步。

19、事实上，利用将对勾函数进行选择可以得到标准的双曲线方程。也就是说，对勾函数是双曲线，这个利用二阶矩阵的变换也是可以得到的。

20、另外对于二次曲线，他只可能是以下几种情况：圆，椭圆，双曲线，抛物线，或者是两条直线。

21、由对勾函数的图像看出来，非双曲线莫属了。

22、面对这个函数 f(x)=ax+b/x,我们应该想得更多，需要我们深入探究：

23、⑴它的单调性与奇偶性有何应用？而值域问题恰好与单调性密切相关，所以命题者首先想到的问题应该与值域有关；

24、⑵函数与方程之间有密切的联系，所以命题者自然也会想到函数与方程思想的运用；

25、⑶众所周知，双曲线中存在很多定值问题，所以很容易就想到定值的存在性问题。因此就由特殊引出了一般结论；继续拓展下去，用所猜想、探索的结果来解决较为复杂的函数最值问题。能否与均值有关系。

二、双勾函数是什么意思

1、以原点中心对称，类似勾的函数y=x+p/x

2、性质当p>0时,它的图象是分布在一、三象限的两条抛物线，都不能与X轴、Y轴相交，为奇函数。

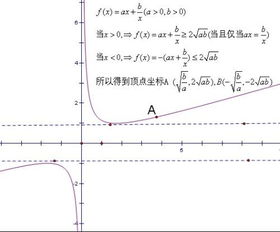
3、对于第一象限的情况：以（√p,2√p）为顶点，在（0，√p]上是减函数，在[√p，+∞）上是增函数，开口向上；

4、第三象限内以（-√p,-2√p）为顶点，在（－∞，-√p],是增函数，在[-√p,0)是减函数，开口向下。

5、其中顶点的纵坐标是由对函数使用均值不等式后得到的。

6、在第一象限的图像，当x越小，即越接近于0时，

7、图像左侧就越趋向Y轴+∞，但不相交;

8、图像右侧就越接近直线y=x正半支，但不相交。

9、在第三象限的图像，当x越大，即越接近于0时，

10、图像右侧就越趋向Y轴－∞，但不相交;

11、图像左侧就越接近直线y=x负半支，但不相交。

12、即渐近线有Y轴，和直线y=x。第一象限：(√p，2√p)

三、什么是双勾函数

在高中数学中函数f（x）=ax+b/x（a,b）〉0）经常会遇到，因为利用它可以考查不等式、最值、函数的单调性、函数的值域,函数的奇偶性等问题．对选择填空题极有帮助，可加快解题速度，由于它的图象在直角坐标系中的形状大致像两个关于原点对称的’双勾”，所以往往被人们亲切的称为“双勾”函数，由于又像耐克的标志，所以又戏称为“耐克函数”。

当函数表达式为y=qx+p/x，我们可以提取出 q，使它成为y=q(x+ p/qx),这样依旧可以由性质上去观察函数。

1.奇偶性：当p>0时,它的图象是分布在一、三象限的两条抛物线，都不能与X轴、Y轴相交，为奇函数。

当p<0时,它的图象是分布在二、四象限的两条抛物线，都不能与X轴、Y轴相交，也为奇函数

2.单调性：对于第一象限的情况：以（√p,2√p）为顶点，在（0，√p]上是减函数，在[√p，+∞）上是增函数，开口向上；

第三象限内以（-√p,-2√p）为顶点，在（－∞，-√p],是增函数，在[-√p,0)是减函数，开口向下。

其中顶点的纵坐标是由对函数使用均值不等式后得到的。

在第一象限的图像，当x越小，即越接近于0时，图像左侧就越趋向Y轴+∞，但不相交;

当x越大，即越趋向+∞时，图像右侧就越接近直线y=x正半支，但不相交。

在第三象限的图像，当x越大，即越接近于0时，图像右侧就越趋向Y轴－∞，但不相交;

当x越小，即越趋向－∞时，图像左侧就越接近直线y=x负半支，但不相交。

3.最值：最值的求法一是利用函数的单调性，二是均值不等式，三是特殊的单调性如求函数Y=(X^2+5)/squ(X^2+4)的最值。实际上用的就是单调性。

顶点的求法是用均值不等式来求的Y=X+P/X（P>0）

当X>0时由均值不等式可知Y=（X+P/X）>=2squ(X*P/X)=2√p

当且仅当X=P/X即X=√p时等号成立。