最优二叉树

一、最优二叉树

1、．树的路径长度树的路径长度是从树根到树中每一结点的路径长度之和在结点数目相同的二叉树中完全二叉树的路径长度最短

2、．树的带权路径长度(Weighted Path Length of Tree简记为WPL)结点的权在一些应用中赋予树中结点的一个有某种意义的实数结点的带权路径长度结点到树根之间的路径长度与该结点上权的乘积树的带权路径长度(Weighted Path Length of Tree)定义为树中所有叶结点的带权路径长度之和通常记为其中 n表示叶子结点的数目w i和l i分别表示叶结点k i的权值和根到结点ki之间的路径长度树的带权路径长度亦称为树的代价

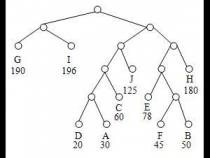
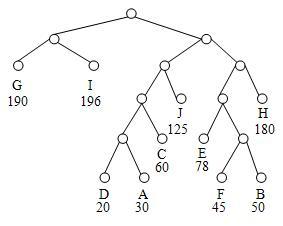
3、．最优二叉树或哈夫曼树在权为wl w… wn的n个叶子所构成的所有二叉树中带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树【例】给定个叶子结点a b c和d分别带权和构造如下图所示的三棵二叉树(还有许多棵)它们的带权路径长度分别为(a)WPL=*+*+*+*=(b)WPL=*+*+*+*=(c)WPL=*+*+*+*=其中(c)树的WPL最小可以验证它就是哈夫曼树

4、注意①叶子上的权值均相同时完全二叉树一定是最优二叉树否则完全二叉树不一定是最优二叉树②最优二叉树中权越大的叶子离根越近③最优二叉树的形态不唯一 WPL最小

5、．哈夫曼算法哈夫曼首先给出了对于给定的叶子数目及其权值构造最优二叉树的方法故称其为哈夫曼算法其基本思想是()根据给定的n个权值w l w… wn构成n棵二叉树的森林F={T T… T n}其中每棵二叉树T i中都只有一个权值为w i的根结点其左右子树均空()在森林F中选出两棵根结点权值最小的树(当这样的树不止两棵树时可以从中任选两棵)将这两棵树合并成一棵新树为了保证新树仍是二叉树需要增加一个新结点作为新树的根并将所选的两棵树的根分别作为新根的左右孩子(谁左谁右无关紧要)将这两个孩子的权值之和作为新树根的权值()对新的森林F重复()直到森林F中只剩下一棵树为止这棵树便是哈夫曼树用哈夫曼算法构造哈夫曼树的过程见【动画演示】注意①初始森林中的n棵二叉树每棵树有一个孤立的结点它们既是根又是叶子② n个叶子的哈夫曼树要经过n次合并产生n个新结点最终求得的哈夫曼树***有 n个结点③哈夫曼树是严格的二叉树没有度数为的分支结点．哈夫曼树的存储结构及哈夫曼算法的实现（）哈夫曼树的存储结构用一个大小为 n的向量来存储哈夫曼树中的结点其存储结构为#define n//叶子数目#define m*n//树中结点总数 typedef struct{//结点类型 float weight//权值不妨设权值均大于零 int lchild rchild parent//左右孩子及双亲指针}HTNode typedef HTNode HuffmanTree[m]//HuffmanTree是向量类型注意因为C语言数组的下界为故用表示空指针树中某结点的lchild rchild和parent不等于时它们分别是该结点的左右孩子和双亲结点在向量中的下标这里设置parent域有两个作用其一是使查找某结点的双亲变得简单其二是可通过判定parent的值是否为来区分根与非根结点

6、（）哈夫曼算法的简要描述在上述存储结构上实现的哈夫曼算法可大致描述为(设T的类型为HuffmanTree)()初始化将T[．．m ]中 n个结点里的三个指针均置为空(即置为)权值置为()输人读人n个叶子的权值存于向量的前n个分量(即T[．．n ])中它们是初始森林中n个孤立的根结点上的权值()合并对森林中的树共进行n次合并所产生的新结点依次放人向量T的第i个分量中(n≤i≤m)每次合并分两步①在当前森林T[．．i ]的所有结点中选取权最小和次小的两个根结点[p ]和T[p ]作为合并对象这里≤p p≤i②将根为T[p ]和T[p ]的两棵树作为左右子树合并为一棵新的树新树的根是新结点T[i]具体操作将T[p ]和T[p ]的parent置为i将T[i]的lchild和rchild分别置为p和p新结点T[i]的权值置为T[p ]和T[p ]的权值之和注意合并后T[pl]和T[p ]在当前森林中已不再是根因为它们的双亲指针均已指向了T[i]所以下一次合并时不会被选中为合并对象哈夫曼算法模拟演示过程【参见动画模拟】

7、（）哈夫曼算法的求精 void CreateHuffmanTree(HuffmanTree T){//构造哈夫曼树 T[m ]为其根结点 int i p p InitHuffmanTree(T)//将T初始化 InputWeight(T)//输入叶子权值至T[．．n ]的weight域 for(i=n i<m i++){//共进行n次合并新结点依次存于T[i]中 SelectMin(T i&p&p)//在T[．．i ]中选择两个权最小的根结点其序号分别为p和p T[p ] parent=T[p ] parent=i TIi] child=p//最小权的根结点是新结点的左孩子 T[j] rchild=p//次小权的根结点是新结点的右孩子 T[i] weight=T[p ] weight+T[p ] weight}// end for}上述算法中调用的三个函数【参见练习】【例】以个权值为例执行CreateHuffmanTree求最优二叉树的过程【参见动画模拟】

二、c语言,二叉树求解～

1、先考虑度为2的结点，第一层1个，第二层2个，第三层4个，第四层8个，第五层8个，共23个。

2、然后第5层还有8个空位，先假设为叶子节点，即度为0。第五层满，目前总共31个结点。

3、然后第五层的8个度为2的结点可以引申出16个叶子结点，总共47个，以满足题意，假设成立。

4、当然比较简单的题画图会很好解。

三、二叉树(C语言)

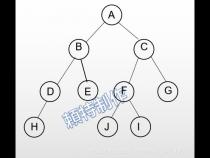
这个问题，可以看成完全二叉树，有性质有节点i的父节点为： i/2.

而题目要求的意思也就是找到两个节点的公共父节点。（含可能为其中一个节点）

找到较大的那个，（循环的，因不断改变，所以需不断比较）

做x=x/2；（假设此时x较大,x为int型）

（因马上断电，不给代码了，思路就是这样。。。）