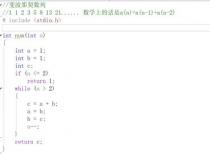
斐波那契数列c语言

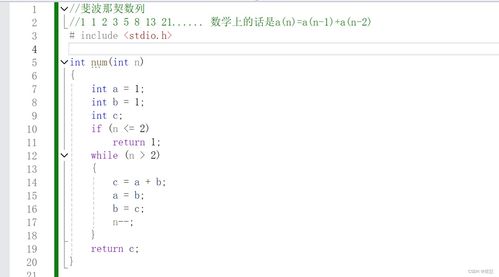
一、斐波那契数列c语言

//函数用于计算斐波那契数列的第n项值

} else{//递归计算斐波那契数列的值

int n= 10;//假设需要计算第10项的斐波那契数列值

斐波那契数列定义：斐波那契数列是一个序列，其中每个数字是前两个数字的和。序列通常以这种方式开始：0、1，之后的每个数字都是前两个数字的和。例如，接下来的数字是0+1=1，然后是1+1=2，依此类推。在上面的代码中，我们创建了一个函数来计算斐波那契数列的任意项。对于数列的第一个和第二个元素，我们直接返回它们作为基本情形处理。对于其他的项，我们使用递归方法来计算它们，即每一项的值等于前两项之和。在main函数中，我们调用fibonacci函数来计算并打印斐波那契数列的第n项值。因为代码中没有设置特别大的限制，用户可以自由地改变变量n来求任意项的值。注意这种方法在计算大数时会消耗大量的时间和资源，可以通过其他算法如动态规划优化来改进效率。

二、求用C语言表达斐波那契数列

斐波那契数列，又称黄金分割数列，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

C语言是一门通用计算机编程语言，应用广泛。C语言的设计目标是提供一种能以简易的方式编译、处理低级存储器、产生少量的机器码以及不需要任何运行环境支持便能运行的编程语言。

尽管C语言提供了许多低级处理的功能，但仍然保持着良好跨平台的特性，以一个标准规格写出的C语言程序可在许多电脑平台上进行编译，甚至包含一些嵌入式处理器（单片机或称MCU）以及超级电脑等作业平台。

二十世纪八十年代，为了避免各开发厂商用的C语言语法产生差异，由美国国家标准局为C语言订定了一套完整的国际标准语法，称为ANSI C，作为C语言最初的标准。

三、斐波那契数列通项公式,详细过程。

即斐波那契数列,“斐波那契数列”的发明者，是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci，生于公元1170年，卒于1240年。籍贯大概是比萨）。他被人称作“比萨的列昂纳多”。1202年，他撰写了《珠算原理》(Liber Abaci)一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点相当于今日的阿尔及利亚地区，列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。

斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21……

这个数列从第三项开始，每一项都等于前两项之和。它的通项公式为：(1/√5)*{[(1+√5)/2]^n- [(1-√5)/2]^n}【√5表示根号5】

很有趣的是：这样一个完全是自然数的数列，通项公式居然是用无理数来表达的。

比如：随着数列项数的增加，前一项与后一项之比越逼近黄金分割0.6180339887……

还有一项性质，从第二项开始，每个奇数项的平方都比前后两项之积多1，每个偶数项的平方都比前后两项之积少1。

如果你看到有这样一个题目：某人把一个8*8的方格切成四块，拼成一个5*13的长方形，故作惊讶地问你：为什么64＝65？其实就是利用了斐波那契数列的这个性质：5、8、13正是数列中相邻的三项，事实上前后两块的面积确实差1，只不过后面那个图中有一条细长的狭缝，一般人不容易注意到。

如果任意挑两个数为起始，比如5、-2.4，然后两项两项地相加下去，形成5、-2.4、2.6、0.2、2.8、3、5.8、8.8、14.6……等，你将发现随着数列的发展，前后两项之比也越来越逼近黄金分割，且某一项的平方与前后两项之积的差值也交替相差某个值。

斐波那契数列的第n项同时也代表了集合{1,2,...,n}中所有不包含相邻正整数的子集个数。

斐波那契数列又因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入，故又称为“兔子数列”。

一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔都不死，那么一年以后可以繁殖多少对兔子？

我们不妨拿新出生的一对小兔子分析一下：

第一个月小兔子没有繁殖能力，所以还是一对;

两个月后，生下一对小兔民数共有两对;

三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对;

兔子对数：1123581321345589144233

表中数字1，1，2，3，5，8－－－构成了一个数列。这个数列有关十分明显的特点，那是：前面相邻两项之和，构成了后一项。

这个数列是意大利中世纪数学家斐波那契在＜算盘全书＞中提出的，这个级数的通项公式，除了具有a(n+2)=an+a(n+1)/的性质外，还可以证明通项公式为：an=1/√[（1＋√5/2) n-(1-√5/2) n](n=1,2,3.....）

【斐波那挈数列通项公式的推导】

斐波那契数列：1，1，2，3，5，8，13，21……

如果设F(n)为该数列的第n项(n∈N+)。那么这句话可以写成如下形式：

F(1)=F(2)=1,F(n)=F(n-1)+F(n-2)(n≥3)

通项公式的推导方法一：利用特征方程

∴F(n)=(1/√5)*{[(1+√5)/2]^n- [(1-√5)/2]^n}【√5表示根号5】

通项公式的推导方法二：普通方法

使得F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]

F(n)-r*F(n-1)=s*[F(n-1)-r*F(n-2)]

F(n-1)-r*F(n-2)=s*[F(n-2)-r*F(n-3)]

F(n-2)-r*F(n-3)=s*[F(n-3)-r*F(n-4)]

F(n)-r*F(n-1)=[s^(n-2)]*[F(2)-r*F(1)]

= s^(n-1)+ r*s^(n-2)+ r^2*F(n-2)

= s^(n-1)+ r*s^(n-2)+ r^2*s^(n-3)+ r^3*F(n-3)

= s^(n-1)+ r*s^(n-2)+ r^2*s^(n-3)+……+ r^(n-2)*s+ r^(n-1)*F(1)

= s^(n-1)+ r*s^(n-2)+ r^2*s^(n-3)+……+ r^(n-2)*s+ r^(n-1)

（这是一个以s^(n-1)为首项、以r^(n-1)为末项、r/s为公差的等比数列的各项的和）

=[s^(n-1)-r^(n-1)*r/s]/(1-r/s)

r+s=1,-rs=1的一解为 s=(1+√5)/2, r=(1-√5)/2

则F(n)=(1/√5)*{[(1+√5)/2]^n- [(1-√5)/2]^n}

printf("F%d==%d\n", i, fib);

write('F', i,'=', fib[i ]);

对于斐波那契数列1,1,2,3,5,8,13…….有如下定义

可见该矩阵的乘法完全符合斐波那契数列的定义

斐波那契数列的某一项F(n)=(BC^(n-2))1

这就是斐波那契数列的矩阵乘法定义.

另矩阵乘法的一个运算法则A¬^n(n为偶数)=A^(n/2)* A^(n/2).

时间效率：O(logn)，比模拟法O(n)远远高效。

{变量matrix是二阶方阵, matrix是矩阵的英文}

matrix=array[1..2,1..2] of qword;

function multiply(x,y:matrix):matrix;

temp[1,1]:=x[1,1]*y[1,1]+x[1,2]*y[2,1];

temp[1,2]:=x[1,1]*y[1,2]+x[1,2]*y[2,2];

temp[2,1]:=x[2,1]*y[1,1]+x[2,2]*y[2,1];

temp[2,2]:=x[2,1]*y[1,2]+x[2,2]*y[2,2];

function getcc(n:integer):matrix;

if odd(n) then exit(multiply(temp,c))

F(n)= [(( sqrt( 5)+ 1)/ 2) ^ n ]

其中[ x ]表示取距离 x最近的整数。