求一元二次方程的根c语言

一、求一元二次方程的根c语言

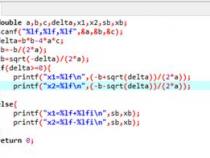
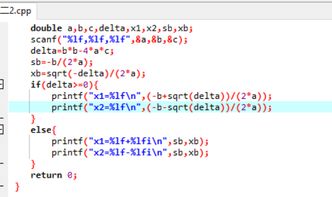
1、c语言一元二次方程编程是#include<iostream>。#include<cmath>。usingnamespacestd。intmain()。{floata,b,c;floatx1,x2; cin>a>>b>>c;floatdlt=b*b-4*a*c;if(dlt>=0){x1=-b/2/a+sqrt(dlt)。/2/ax2=-b/2/a-sqrt(dlt)/2/a。

2、形如x=p或（nx+m）=p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．如果方程化成x²=p的形式，那么可得x=±p；(x²=p,x=±根号p）如果方程能化成（nx+m）=p（p≥0）的形式，那么nx+m=±p。

3、C语言包含的各种控制语句仅有9种，关键字也只有32个，程序的编写要求不严格且以小写字母为主，对许多不必要的部分进行了精简。

4、实际上，语句构成与硬件有关联的较少，且C语言本身不提供与硬件相关的输入输出、文件管理等功能，如需此类功能，需要通过配合编译系统所支持的各类库进行编程，故c语言拥有非常简洁的编译系统。

5、提供的控制语句具有结构化特征，如for语句、if...else语句和switch语句等。可以用于实现函数的逻辑控制，方便面向过程的程序设计。

二、c语言二分法求方程的根的算法

如果连续函数在给定区间不单调，很有可能中值*下界值和中值*上界值都大于0，那么会跳出认为没有根，而事实上很有可能这个中值点靠近函数极点。

而真正用二分法求给定区间的思路是：

首先为函数求导，算出导函数的零点，然后再判断零点性质，最后将函数区间分为单调递增和单调递减间隔的形式，对每一段进行二分法求根。

#define_VALUE(x)(2*x*x*x-4*x*x+3*x-6)

intgetRoot(doublelower,doubleupper,double*result);

if(getRoot(DEFAULT_LOWER,DEFAULT_UPPER,&root))

intgetRoot(doublelower,doubleupper,double*result)

if(_VALUE(lower)*_VALUE(*result)<=0)

returngetRoot(lower,*result,result);

elseif(_VALUE(*result)*_VALUE(upper)<=0)

returngetRoot(*result,upper,result);

三、求解一元三次方程的C语言程序

可以使用二分法，弦截法，牛顿法，以前写的，希望对LZ有帮助。

用弦截法求方程F(x)=X^3-5X^2+16X-80=0的根。

（1）取两个不同的点x1,x2,如果f(x1)和f(x2)符号相反，则（x1,x2）区间内必有一个根。如果f(x1)和f(x2)同符号，则应改变x1,x2，直到f(x1)和f(x2)异号为止。注意x1和x2的值不应差太大，以保证（x1,x2）区间内只有一根。

（2）连接（x1,f(x1)）和（x2,f(x2)）两点，此线交x轴于x，x的坐标可以用下式求出：x=(x1*f(x2)-x2*f(x1))/f(x2)-f(x1),

（3）若f(x)和f(x1)同符号，则根必在(x,x2)内，此时将x作为新的x1;如果f(x)和f(x2)同符号，则表示根在(x1,x)，此时将x作为新的x2。

（4）重复步骤（2）和（3），知道|f(x)|<e,e是一个很小的数，例如10^-6;

float xpoint(float x1,float x2)

{//求(x1,f(x1)和(x2,f(x2))连线与x轴的交点

y=(x1*f(x2)-x2*f(x1))/(f(x2)-f(x1));

printf("input x1,x2:\n");

printf("a root of equation is%8.4f\n",x);

牛顿迭代法又称牛顿切线法，它采用以下方法求根：先任意设定一个与真实的根接近的值x0作为第一个近似根，由x0求出f(x0)，过(x0,f(x0))点做f(x)的切线，交x轴于x1，把它作为第二次近似根，再由x1求出f(x1)，再过(x1,f(x1))点做f(x)的切线，交x轴于x2，再求出f(x2)，再作切线……如此继续下去，直到足够接近真正的x为止。

其中f'(X0)是函数在X0处的斜率，也就是在X0处的导数。

float f(float a,float b,float c,float d,float x)

float f1(float a,float b,float c,float x)

float root(float a,float b,float c,float d)

x1=x0-f(a,b,c,d,x0)/f1(a,b,c,x0);

printf("input four float numbers:\n");

scanf("%f%f%f%f",&a,&b,&c,&d);

printf("%.1fX^3+%.1fX^2+%.1fX+%.1f=0 its root near x=1.5 is:%.4f\n",a,b,c,d,x);