C语言 1到N的乘积

发布时间:2025-05-11 23:04:08 发布人:远客网络

C语言 1到N的乘积

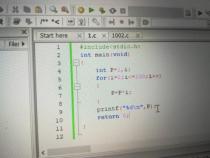
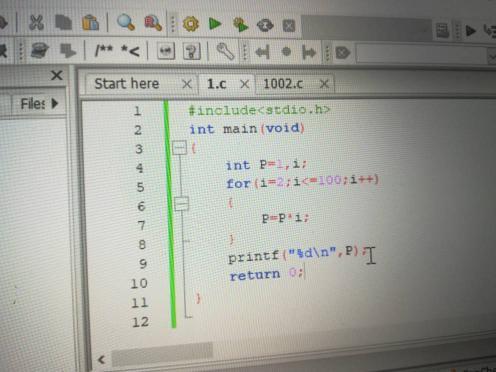
1、C语言中计算1到N的乘积，可以通过一个简单的程序实现。下面是一个示例：

2、 for(i= 1; i<= N; i++) s*= i;

3、这段代码首先读取一个整数N，然后使用一个循环将1到N的整数相乘。这里使用了变量s来存储乘积的结果，初始值为1。每次循环中，将当前的i值乘以s，然后更新s的值。循环结束后，s中存储的就是1到N的乘积。

4、在讨论阶乘时，我们经常提到一个正整数的阶乘是所有小于及等于该数的正整数的积。阶乘的概念最早由基斯顿·卡曼在1808年提出，用符号n!表示。例如，5的阶乘写作5!，计算结果为1×2×3×4×5=120。

5、阶乘定义的引入不仅是为了方便数学表达，也因为它在组合数学、概率论等领域有广泛的应用。例如，在组合数学中，计算从n个不同元素中取出k个元素的组合数时，就会用到阶乘。另外，概率论中的许多公式也需要使用阶乘。

6、需要特别注意的是，0的阶乘被定义为1。这一定义并不是没有意义的，而是为了保证某些数学公式的正确性。比如，在组合数学中，从n个不同元素中取出0个元素的组合数是1，这与阶乘定义一致。

7、阶乘还可以通过递归的方式定义：0!= 1，n!=(n-1)!× n。这种定义方式简洁且易于理解，对于编程实现来说也非常方便。

8、总结来说，1到N的乘积可以通过简单的C语言程序实现，而阶乘的概念及其定义在数学和计算机科学中有广泛的应用，不仅方便了数学表达，也极大地简化了某些计算。

1、若然一矩阵的列数与另一矩阵的行数相等，则可定义这两个矩阵的乘积。如A是m×n矩阵和B是n×p矩阵，它们是乘积AB是一个m×p矩阵，其中

2、(AB)[i,j]=A[i,1]*B[1,j]+A[i,2]*B[2,j]+...+A[i,n]*B[n,j]对所有i及j。

3、(AB)C=A(BC)对所有k×m矩阵A,m×n矩阵B及n×p矩阵C("结合律").

4、(A+B)C=AC+BC对所有m×n矩阵A及B和n&tiems;k矩阵C("分配律")。

5、C(A+B)=CA+CB对所有m×n矩阵A及B和k×m矩阵C("分配律")。

6、要注意的是：可置换性不一定成立，即有矩阵A及B使得AB≠BA。

7、Q=M*N(Q的行数和M相同，列数和N相同)

8、其中，M是m1*n1矩阵，N是m2*n2矩阵。当n1=m2时有：

9、for(k=1;k<=n1;++k)Q[i][j]+=M[i][k]*N[k][j];

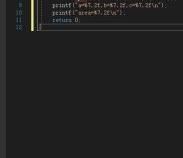
1、C语言代码实现了一个简单的程序，用于计算1至100的数的和值和乘积。程序首先定义了两个变量s和f，分别用于存储和值和乘积。在for循环中，变量i从1迭代到100，每次迭代时，s累加当前值i，f乘以当前值i。最后，程序通过printf函数输出计算结果。

2、具体来说，s变量用于累加1到100之间的所有整数。例如，当i为1时，s初始化为0，然后s加1，变为1。接下来，当i为2时，s加2，变为3，以此类推。最终，s将包含1到100之间所有整数的和。

3、另一方面，f变量用于计算1到100之间的所有整数的乘积。初始时，f设置为1。在第一次迭代中，f乘以1，保持不变。然而，当i变为2时，f乘以2，变为2。随着循环的继续，f将乘以每个新值i，最终包含1到100之间所有整数的乘积。

4、通过这个简单的程序，我们可以看到C语言的强大之处，它可以轻松地执行复杂的数学运算。此外，这个程序也展示了for循环在处理一系列数字时的灵活性。

5、值得注意的是，s和f分别使用double数据类型，以确保在计算过程中能够处理较大的数值。虽然在计算1到100之间的和时，s的值不会溢出，但在计算乘积时，f可能会迅速增长，导致溢出。因此，在实际应用中，应根据具体需求选择合适的数据类型。

6、最后，通过输出语句，程序展示了1到100之间所有整数的和值和乘积。这对于理解和验证程序的正确性非常有用。

7、这个程序可以作为学习C语言的基础示例，帮助初学者理解循环、变量和基本的数学运算。通过这种方式，我们可以逐步构建更复杂和功能强大的程序。